P3581 [POI 2015] CZA

听 aqz 大佬说，掌握了这道题状压维护相对位置的计数方法，大部分的计数都可以这么做（？）。

首先讨论 p \leq 2 的情况，p = 0 答案即为 [n = 1]；p = 1 时，要么 n = 1，要么 n = 2 且没有任何限制。

讨论 p = 2 的情况，手模发现只有两种情况，把 1 固定，然后两边分别放上 2 和 3，交替进行，以此类推，顺时针一个逆时针一个，有个坑就是 n = 1 的情况，需要特判只有 1 种情况。

if (p == 2) {
    if (n == 1) {
        write(1), puts("");
        return 0;
    }
    int l = 1, r = n;
    for (int i = 1; i <= n; ++i)
        if (i & 1) a[l++] = i;
        else a[r--] = i;
    a[n + 1] = 1;
    bool key = true;
    for (int i = 1; i <= n; ++i)
        key &= chk(a[i], a[i + 1]);
    ans += key;
    key = true;
    for (int i = 1; i <= n; ++i)
        key &= chk(a[i + 1], a[i]);
    ans += key;
    write(ans), puts("");
}

然后讨论 p = 3 的情况，我菜，学习了一个及其厉害的做法。

发现从大往小插入，那么如果当前插入 i，能够与其相邻的只有 i + 1，i + 2，i + 3，i - 1，i - 2，i - 3，后边三个不考虑，等插入的时候再考虑即可。

所以考虑维护 i + 1，i + 2，i + 3，因为要插入 i，只能插入到其中两者中间，所以维护两者之间是否有其他元素，如果有其他元素，那么肯定是不能插入 i 的，否则是可以的，看起来差不多可以状压了。

下面假设为顺时针，逆时针同理。

那么不妨设 i + 1 与 i + 2 中间的位置为 1 号位；i + 2 与 i + 3 中间的位置为 1 号位；i + 3 与 i + 1 中间的位置为 1 号位。

那么现在的圆桌可以抽象成这个样子。

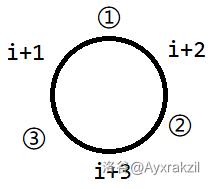
考虑插入 i，插入 i 后，后面所有的元素是不可以与 i + 3 相邻的，所以需要删去，这时候就需要判断一下它能否与相邻两个元素相邻，需要注意的是并不需要判断 i 与相邻两者是否可以相邻，只需插入一个没有任何元素的空位即可，因为此时维护的只是相对位置，后面可能还会往里面插入，等将其删去的时候再判断即可，而这个判断就是前面说的那个判断。

值得注意的是，插入 1 号位会使得顺时针变成逆时针，逆时针变成顺时针。

然后插入完之后要封口，也就是将最后没有判断的元素判断一下，这个也是跟前面差不多。

这里设 f_{i, d, st} 表示考虑到 i，此时是否是顺时针，以及此时的空闲位置。

code

#include <bits/stdc++.h>

const int N = 1e6 + 5, mod = 1e9 + 7;

int n, k, p, u, v;
bool vis[N][10];
int a[N];
int ans;
int f[N][2][8];

int read() {
    int res = 0, i = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-') i = -i;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = getchar();
    }
    return res * i;
}

void write(int x) {
    if (x < 0) {
        putchar('-');
        x = -x;
    }
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}

inline void add(int& x, int y) {
    x = (x + y >= mod) ? (x + y - mod) : (x + y);
}

inline bool chk(int i, int j) {
    return ((abs(i - j) <= p) && (!vis[j][j - i + 3]));
}

bool check(int i, int d, int st, int p) {
    if (d) {
        if (p == 1) return ((!(st & 4) || chk(i + 3, i + 1)) && (!(st & 2) || chk(i + 2, i + 3)));
        else if (p == 2) return (chk(i, i + 3) && (!(st & 4) || chk(i + 3, i + 1)));
        else return (chk(i + 3, i) && (!(st & 2) || chk(i + 2, i + 3)));
    } else {
        if (p == 1) return ((!(st & 4) || chk(i + 1, i + 3)) && (!(st & 2) || chk(i + 3, i + 2)));
        else if (p == 2) return (chk(i + 3, i) && (!(st & 4) || chk(i + 1, i + 3)));
        else return (chk(i, i + 3) && (!(st & 2) || chk(i + 3, i + 2)));
    }
}

bool checklst(int i, int d, int st, int p) {
    if (i > 1) return true;
    if (d) {
        if (p == 1) return (chk(2, 1) && chk(1, 3));
        else if (p == 2) return ((!(st & 1) || chk(2, 3)) && chk(3, 1));
        else return ((!(st & 1) || chk(2, 3)) && chk(1, 2));
    } else {
        if (p == 1) return (chk(1, 2) && chk(3, 1));
        else if (p == 2) return ((!(st & 1) || chk(3, 2)) && chk(1, 3));
        else return ((!(st & 1) || chk(3, 2)) && chk(2, 1));
    }
}

void solve() {
    f[n - 2][0][7] = f[n - 2][1][7] = 1;
    for (int i = n - 2; i > 1; --i)
        for (int d = 0; d <= 1; ++d)
            for (int st = 0; st < 8; ++st) {
                if (!f[i][d][st]) continue;
                if ((st & 1) && check(i - 1, d, st, 1) && checklst(i - 1, d, st, 1))
                    add(f[i - 1][d ^ 1][5], f[i][d][st]);
                if ((st & 2) && check(i - 1, d, st, 2) && checklst(i - 1, d, st, 2))
                    add(f[i - 1][d][4 | ((st & 1) << 1)], f[i][d][st]);
                if ((st & 4) && check(i - 1, d, st, 3) && checklst(i - 1, d, st, 3))
                    add(f[i - 1][d][1 | ((st & 1) << 1)], f[i][d][st]);
            }
    for (int d = 0; d <= 1; ++d)
        for (int st = 0; st < 8; ++st)
            add(ans, f[1][d][st]);
    write(ans), puts("");
}

signed main() {
    n = read(), k = read(), p = read();
    for (int i = 1; i <= k; ++i) {
        u = read(), v = read();
        if (abs(u - v) <= p)
            vis[u][u - v + 3] = true;
    }
    if (p == 0) {
        write(n == 1), puts("");
    } else if (p == 1) {
        write(n == 1 || n == 2 && k == 0), puts("");
    } else if (p == 2) {
        if (n == 1) {
            write(1), puts("");
            return 0;
        }
        int l = 1, r = n;
        for (int i = 1; i <= n; ++i)
            if (i & 1) a[l++] = i;
            else a[r--] = i;
        a[n + 1] = 1;
        bool key = true;
        for (int i = 1; i <= n; ++i)
            key &= chk(a[i], a[i + 1]);
        ans += key;
        key = true;
        for (int i = 1; i <= n; ++i)
            key &= chk(a[i + 1], a[i]);
        ans += key;
        write(ans), puts("");
    } else solve();
    return 0;
}

坑点，p == 2 && n == 1 的特判，不用开 long long，记录不能相邻的只需要记录编号之差绝对值 \leq p 的即可，用 unordered_map 会 MLE，以及能加括号的时候就加上括号，少装，好像自己真的掌握了运算优先级。