很厉害啊,我认为得写一写自己的见解。
不过难免会有错误的地方,请指出。
感谢 aqz 奆佬 orz。
唉,我真傻,真的,第一篇题解看半天看不懂。
前置知识:划分数的 n\sqrt{n} 求法
求 1 \sim n 中选几个数加起来为 n 并且不重复选同一个数的方案数。
简单的想法是 01 背包,这是 O(n^2) 的。
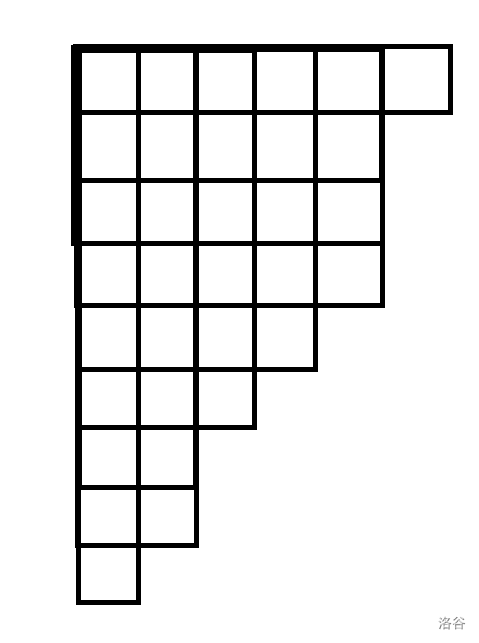
如果每一列代表选一个数,这张图形象地描绘了选择了 1, 4, 5, 6, 8, 9 的情况。
如果对其进行转置,横过来看每一个数,会发现为了保证原本概念上的每个数只能选一次,转置后,变成了相邻的两行最多相差 1,也就是对于每一个行的长度 i 必须要选择一次,而没上限,可以选多次。
于是就成了一个每个长度至少选一次的完全背包。
那么复杂度是如何降到 O(n\sqrt{n}) 的呢?通过利用每个长度至少选一次的性质,发现最长的一行的长度 i 必须满足 \frac{i \times (i + 1)}{2} \leq n,这样的 i 只有 O(\sqrt{n}) 个。
思考原题目,考虑选出的一个序列 a,它所能表示的上界是 \sum a_i,如果所能表示的数能够做到从 0 连续到达上界,那么需要保证 \forall k \in [0, \sum a_i], (\sum [a_i \leq k]a_i) \geq k,证明考虑反证,如果其 < k,那么剩下的元素都是 > k 的,导致了 k 永远无法被凑出来。
设 f_i 为保证能表示出来 1 \sim i 所有数并且所选数之和为 i 的方案数,那么答案便是 2^n - \sum f_i \times 2^{n - i - 1},钦定 i + 1 不选,剩下随便选,这样 i + 1 无法被表示,1 \sim i 都能被表示,这样就能让所有不合法的方案在第一个不合法位置被减去。
f_i 看起来很难求解,于是正难则反,考虑容斥。
设 g_i 表示选若干数然后其和为 i,但不用保证任何其它条件的方案数。
g_i 就是划分数,根据前置知识,这是可以在 O(n\sqrt{n}) 的复杂度求得的。
然后 f_i = g_i - \sum_j f_j \times val(j, i),类似答案的求法,容斥,钦定 j + 1 不选且不能被表示,然后再从 [j + 2, i] 中选择若干,和为 i - j,其方案数即为 val(j, i)。
就到了我认为最难的地方,想了许久都没想明白,因为我是废物。
设 h_i = \sum_j f_j \times val(j, i),那么上式即为 f_i = g_i - h_i。
考虑求得 h_i,这个东西很像划分数啊,那么该怎么求呢?首先前面已经有 j 了,然后要求从 [j + 2, i] 中选择,所以整体值域上减去 j + 2,就变成 j + i \times (j + 2) 了,这就是前提的一个大小,所以 h_{j + i \times (j + 2)} \leftarrow f_j,相当于赋初值的操作,其中 i 即为转置之后当前要选的值,也就是转置之前要选的数的个数,相当于是有 i 个数 \geq j + 2。
既要求 f 同时也要求 h,发现 j + i \times (j + 2) \geq 2j,所以可以倍增,首先递归求出来 1 \sim \lfloor \frac{n}{2} \rfloor,然后进行 \lfloor \frac{n}{2} \rfloor + 2 \sim n 的求解。
.png)
