0. 前言
会添加的吧,会添加的吧?一定会添加的吧!
水文章?
1. 线段树优化建图
区间向区间连边,我们可以利用线段树的优秀区间特性来进行连边。具体来说,我们建立两颗线段树,一颗专门管入边,一颗管出边入边的树父节点向子节点连边(如果子节点向父节点连边,会导致本来只连向该区间的边通过子节点向父节点连的边连向了更大的区间),同理出边的子节点向父节点连边。父子节点之间的边,边权为 0。

总边复杂度大约在 O(m \log n) 级别。
例如上图,本题代码如下:
#include<bits/stdc++.h>
#define int long long
#define ls (p<<1)
#define rs (p<<1|1)
#define pir pair<int,int>
using namespace std;
constexpr int MN=4e6+15,K=6e5;
struct Edge{
int v,w;
};
int n,q,s,dis[MN],pos[MN];
vector<Edge> adj[MN];
bool vis[MN];
inline void add(int u,int v,int w){
adj[u].push_back({v,w});
}
void build(int p,int l,int r){
if(l==r){
pos[l]=p;
return;
}
add(p,ls,0);
add(p,rs,0);
add(ls+K,p+K,0);
add(rs+K,p+K,0);
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
void updatetoqj(int p,int l,int r,int fl,int fr,int u,int w){
if(l>=fl&&r<=fr){
add(u+K,p,w);
return;
}
int mid=(l+r)>>1;
if(mid>=fl) updatetoqj(ls,l,mid,fl,fr,u,w);
if(mid<fr) updatetoqj(rs,mid+1,r,fl,fr,u,w);
}
void updatefromqj(int p,int l,int r,int fl,int fr,int u,int w){
if(l>=fl&&r<=fr){
add(p+K,u,w);
return;
}
int mid=(l+r)>>1;
if(mid>=fl) updatefromqj(ls,l,mid,fl,fr,u,w);
if(mid<fr) updatefromqj(rs,mid+1,r,fl,fr,u,w);
}
void dijk(int begin){
memset(dis,0x3f,sizeof(dis));
priority_queue<pir,vector<pir>,greater<pir>>q;
q.push(pir(0,begin));
dis[begin]=0;
while(!q.empty()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(auto e:adj[u]){
int v=e.v,w=e.w;
if(dis[v]>w+dis[u]){
dis[v]=w+dis[u];
if(!vis[v]) q.push(pir(dis[v],v));
}
}
}
}
signed main(){
cin>>n>>q>>s;
build(1,1,n);
for(int i=1;i<=n;i++){
add(pos[i],pos[i]+K,0);
add(pos[i]+K,pos[i],0);
}
while(q--){
int op,u,fl,fr,w,v;
cin>>op;
if(op==1){
cin>>u>>v>>w;
add(pos[u]+K,pos[v],w);
}else if(op==2){
cin>>u>>fl>>fr>>w;
updatetoqj(1,1,n,fl,fr,pos[u],w);
}else if(op==3){
cin>>u>>fl>>fr>>w;
updatefromqj(1,1,n,fl,fr,pos[u],w);
}
}
dijk(pos[s]+K);
for(int i=1;i<=n;i++){
cout<<(dis[pos[i]]<0x3f3f3f3f3f3f3f3f?dis[pos[i]]:-1)<<" ";
}
return 0;
}
2. 前后缀优化建图
可以用于连边区间序列的前后缀或树上根链的情况。
这一部分优化的是一个点向一整个前缀或后缀连边,暴力连边数可达到惊人的 O(n^2),无法承受。
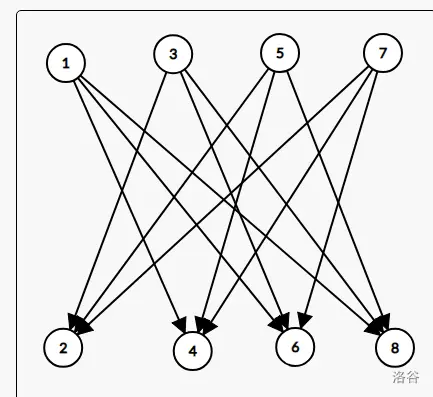
我们通过对于每一个节点 i 建立两个复制节点:pre_{i},suf_{i}。连边为 i \to pre_{i},pre_{i-1} \to pre_{i}。同理于 suf。
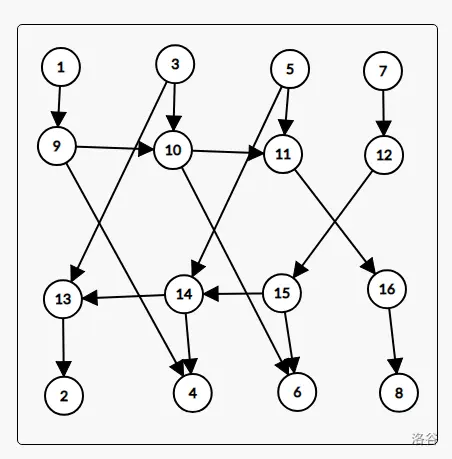
对于树上根链,直接建内向树,连根链末尾即可。
2-sat 加优化建图:
// 注释:DeepseekR1 and V3,WJY
// 可以线段树优化,但是问题是你要开好多个线段树来存储[1,x-1],[x,n]的节点信息,空间很炸裂,但也能做
#include<bits/stdc++.h>
using namespace std;
const int MN=8e6+15;
int n,m,k,dfn[MN],low[MN],vdcc[MN],tot,dcc;
// dfn: DFS序, low: Tarjan算法中的low值,
// vdcc: 强连通分量编号, tot: dfn时间戳, dcc: 强连通分量计数器
vector<int> adj[MN],gp[MN]; //gp: 存储每个部分(题意中的部分)的点
bool vis[MN];
int s[MN],top;
void tarjan(int u){
// tarjan求强联通
low[u]=dfn[u]=++tot;
s[++top]=u;
vis[u]=1;
for(auto v:adj[u]){
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(vis[v]){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
dcc++;
int p;
do
{
p=s[top--];
vdcc[p]=dcc;
vis[p]=0;
} while (p!=u);
}
}
// 以下注释中
// ¬u表示u的否定,即u+n
// u的前缀辅助点,即u+2n
// u的后缀辅助点,即u+3n
int main(){
cin>>n>>m>>k;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
int fu=u+n,fv=v+n;
adj[fu].push_back(v); // 添加边¬u → v
adj[fv].push_back(u); // 添加边¬v → u
}
for(int i=1;i<=k;i++){
int num;
cin>>num;
for(int j=1;j<=num;j++){
int p;
cin>>p;
gp[i].push_back(p);
adj[p].push_back(p+2*n); // 添加边 p → p+2n(前缀变量)
adj[p+3*n].push_back(p+n); // 添加边 p+3n → ¬p(后缀变量)
}
for(int j=1;j<gp[i].size();j++){
int d1=gp[i][j-1],d2=gp[i][j]; // 前一个点和当前点
adj[d1+2*n].push_back(d2+2*n); // 添加边 d1+2n → d2+2n(前缀传递)
adj[d2+3*n].push_back(d1+3*n); // 添加边 d2+3n → d1+3n(后缀传递,可以看图理解)
adj[d1+2*n].push_back(d2+n); // 添加边 d1+2n → ¬d2(前缀已选,d2不可选)
adj[d2].push_back(d1+3*n); // 添加边 d2 → d1+3n(选d2,后缀必须选到d1)
}
}
for(int i=1;i<=n*4;i++){
if(!dfn[i]) tarjan(i);
}
for(int i=1;i<=n;i++){
if(vdcc[i]==vdcc[i+n] || vdcc[i+2*n]==vdcc[i+3*n]){
// 如果i和¬i在同一分量,或前缀和后缀变量在同一分量则环无解
cout<<"NIE";
return 0;
}
}
cout<<"TAK";
return 0;
}
首先这个字典树的边权没有任何卵用,因为题目中已经给出边上的 d_{i} 了。
其次这个题一眼最短时间,说人话就是最短路,考虑 Dijkstra 求最短路,因为这里 SPFA 显然已死(你真的要卡 O(nm)?)。问题转化为如何取去建图,根据题意,通过一条边的边权是如下构成的:
不难注意到题目中慷慨的给我们了字典树,根据字典树上的性质,任意两个点之间的 LCA 节点的深度大小就是这两点的所构成字符串的最长公共前缀长度,那么边权转化为:
但是这里面有一个棘手的地方就是这个 d_{now},因为如果我们真的要在 Dijkstra 上跑的话这个 d_now 是不太好处理的。考虑题目的性质,注意到题目中的点几乎没有任何卵用,因为所有信息都在有向图的边上,那么我们考虑怎么从边上下手。考虑点边互换,将边拆成入点和出点,连边 in \to out,边权为 c_{e}。让后考虑这个 LCA 怎么处理,其实很简单,我们对于第一个边的出点,我们向第二个边的入点连上边权为两个边上的 LCA 权,即 dep\left\{ \operatorname{LCA}(d_{(u,v)},d_{(v,t)}) \right\}。
注意到节点 1 向哪里走都是无代价的,所以对于所有 1 \to a 的边,我们建超级源点 S,让 S \to a,边权为 0 即可。
让后输出最短路长度的时候,答案即为 \min\limits_{b_{e}=i} dis_{out},正确性是显然的。
写完交上去,恭喜你 MLE+TLE。为什么?因为边数最高可到达 O(m^2) 啊,这个时候又要开始优化建图了(悲)。
首先原来的 in \to out 显然是不能动的,我们考虑对 LCA 上下手,注意到我们对于 LCA 上都是一个一个连边的,而 LCA 对于大多数对节点是相同的,这是什么,虚树啊!我们考虑虚树的大小能否支持我们操作,不妨设 S=\left\{ d_{i}| b_{i}=u,a_{i}=u \right\},那么这些边的边权只能是 S 中任意两点 LCA 的深度,根据虚树特性理论,S,中任意两点的 LCA 总共只有 O(|S|) 个,对于所有点,\sum\limits_{u} |S_u|=m,边复杂度 O(m),可以接受。
我们考虑把 LCA 这个点拿出来建虚点,在子树中的节点连一个 LCA 的虚点,让后在从这个虚点连向另外一个虚点,让后在利用虚树进行建边,但是这样边数是 O(n) 的,总边数还是 O(n^2) 的,还是会被卡,考虑怎么优化。
注意到,我们实际上连边都是在子树中的节点连一个 LCA 的虚点,让后在从这个虚点连向另外一个虚点,考虑这个怎么优化。子树的性质,DFN连续。那么,问题转化为 DFS 序上的区间向点连边,点向另外一个连续区间连边,这是什么,线段树优化建图啊!让后就做完了,时间复杂度因为连边是 O(\log n) 的,所以总复杂度是 O(n \log^2 m),我没写因为我有卡常黑历史 www。
能不能再给力一点啊?
可以的!上述过程我们是在暴力枚举 LCA 的,事实上,如果两点间连了一堆的边,但是只有代价最小的边是有用的,剩下都是没太大啥用的,连了也不影响。
我们先把 S 集合求出来,连边的话我们从 [1,i] 的出点向 [i+1,t] 入点,[i+1,t] 出点向 [1,i] 入点连边,其中 t=|S|,这个可以用线段树也可以用神秘的前缀后缀优化建图来做。让后根据上面所说的,只有代价最小的边有用,也就是说对于一个子树区间,只有 \min_{x,y} dep[ \operatorname{lca}(x,y)] 才有用,我们考虑这个代价最小的边怎么连,注意到每次都是某个前缀向后缀连边,或者后缀向前缀连边,为什么,你思考上面线段树的做法。那么,我们建立四个数组:前缀入点、前缀出点、后缀入点、后缀出点。这样的建边是 O(1) 的,时间复杂度是 O(n \log m)。
#include<bits/stdc++.h>
#define int long long
#define pir pair<int,int>
using namespace std;
constexpr int MN=1e6+15,MLOG=20;
struct Edge{
int v,w;
};
struct EDGE{
int a,b,c,d;
}e[MN];
int n,m,K,S,ans[MN],hlca[MN],ntot,prein[MN],preout[MN],sufin[MN],sufout[MN];
vector<int> out[MN],in[MN];
vector<Edge> adj[MN];
vector<pir> vt; // 这是集合 S
namespace Trie{
vector<int> g[MN];
int fa[MN][30],dep[MN],dfn[MN],dfntot;
void triedfs(int u,int pre){
dfn[u]=++dfntot;
fa[u][0]=pre;
dep[u]=dep[pre]+1;
for(int i=1;i<=MLOG;i++){
fa[u][i]=fa[fa[u][i-1]][i-1];
}
for(auto v:g[u]){
triedfs(v,u);
}
}
int lca(int x,int y){
if(dep[x]>dep[y]) swap(x,y);
for(int i=MLOG;i>=0;i--){
if(dep[fa[y][i]]>=dep[x]) y=fa[y][i];
}
if(x==y) return x;
for(int k=MLOG;k>=0;k--){
if(fa[x][k]!=fa[y][k]){
x=fa[x][k],y=fa[y][k];
}
}
return fa[x][0];
}
}using namespace Trie;
namespace Dijkstra{
int dis[MN];
bool vis[MN];
void dijk(int st){
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
priority_queue<pir,vector<pir>,greater<pir>> q;
dis[st]=0;
q.push(pir(0,st));
while(!q.empty()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(auto e:adj[u]){
int v=e.v;
if(dis[v]>dis[u]+e.w){
dis[v]=dis[u]+e.w;
q.push(pir(dis[v],v));
}
}
}
}
}using namespace Dijkstra;
bool cmp(pir x,pir y){
return dfn[x.first]<dfn[y.first];
}
void clear(){
S=MN-3;
ntot=dfntot=0;
memset(dfn,0,sizeof(dfn));
memset(dep,0,sizeof(dep));
memset(fa,0,sizeof(fa));
for(int i=0;i<MN;i++){
in[i].clear();
out[i].clear();
g[i].clear();
adj[i].clear();
}
}
void solve(){
cin>>n>>m>>K;
clear();
ntot=m<<1;
for(int i=1;i<=m;i++){
cin>>e[i].a>>e[i].b>>e[i].c>>e[i].d;
out[e[i].a].push_back(i);
in[e[i].b].push_back(i);
}
for(int i=1;i<K;i++){
int u,v,w;
cin>>u>>v>>w;
g[u].push_back(v);
}
triedfs(1,0);
for(int i=1;i<=m;i++){
adj[i].push_back({i+m,e[i].c});
if(e[i].a==1) adj[S].push_back({i,0});
}
// 以上都是常规建边
for(int i=1;i<=n;i++){
vt.clear();
for(auto p:in[i]) vt.push_back(pir(e[p].d,p+m));
for(auto p:out[i]) vt.push_back(pir(e[p].d,p));
sort(vt.begin(),vt.end(),cmp);
for(int j=0;j<vt.size();j++){ //新建前缀后缀节点
prein[j]=++ntot;
preout[j]=++ntot;
sufin[j]=++ntot;
sufout[j]=++ntot;
}
for(int j=0;j+1<vt.size();j++){
hlca[j]=lca(vt[j].first,vt[j+1].first); // 求出 dfn 排序后的任意两个节点的LCA
adj[prein[j+1]].push_back({prein[j],0}); // 前缀后缀初始化建图
adj[preout[j]].push_back({preout[j+1],0});
adj[sufin[j]].push_back({sufin[j+1],0});
adj[sufout[j+1]].push_back({sufout[j],0});
}
for(int j=0;j<vt.size();j++){
// 前缀建图要分类,别建炸缸了
if(vt[j].second<=m){
adj[sufin[j]].push_back({vt[j].second,0});
adj[prein[j]].push_back({vt[j].second,0});
}
else{
adj[vt[j].second].push_back({sufout[j],0});
adj[vt[j].second].push_back({preout[j],0});
}
}
for(int j=0;j+1<vt.size();j++){
// 连边,这里dep-1是因为根节点dep=1,而lcp是根节点到
// 当前节点的距离,dep[rt]=1,所以要-1
adj[sufout[j+1]].push_back({prein[j], dep[hlca[j]]-1});
adj[preout[j]].push_back({sufin[j+1], dep[hlca[j]]-1});
}
}
dijk(S);
memset(ans,0x3f,sizeof(ans));
for(int i=1;i<=m;i++){
// 暴力枚举
ans[e[i].b]=min(ans[e[i].b],dis[i+m]);
}
for(int i=2;i<=n;i++) cout<<ans[i]<<'\n';
}
signed main(){
int T;
cin>>T;
while(T--){
solve();
}
return 0; // byebye程序
}
3. 后缀树上优化建图
当然是 SAM 做法啦,首先为了求前缀信息直接对反串求后缀自动机。
不难注意到这个支配关系很想一个图中的边,我们思考能不能进行图论建模,但是前缀全部建图是很难受的,但是一个性质,link 树上的祖先在反串上都是它的前缀。
我们记录一下反串每一个位置在后缀自动机上的位置,然后在 link 树上倍增上去找 s[l,r] 对应的节点。我们对于后缀自动机上每一个节点开一个 vector,按照子串长度为第一关键字,是否为 A 类串为第二关键字排序,然后依次连边。让后把后缀自动机父亲结点挂下来的结点向当前结点连一条边。
然后问题就是在 DAG 上求最长路!
其实就是综合利用 link 树上的祖先在反串上都是它的前缀的特性。
大约是 O(Tn \log n)
#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=1e6+15;
int n,na,nb,m,in[MN],tot,dis[MN],a[MN],b[MN],last[MN],fa[MN],pre[31][MN],pos[MN];
long long ans;
bool isa[MN];
string s;
vector<int> adj[MN],g[MN];
struct SAM{
int nxt[MN][26],len[MN],stot,lst;
void init(){
for(int i=0;i<=stot;i++){
fa[i]=len[i]=0;
for(int j=0;j<=30;j++) pre[j][i]=0;
memset(nxt[i],0,sizeof(nxt[i]));
}
stot=lst=1;
}
void expand(int c){
int cur=++stot;
len[cur]=len[lst]+1;
int p=lst;
while(p&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
if(!p){
fa[cur]=1;
}else{
int q=nxt[p][c];
if(len[q]==len[p]+1){
fa[cur]=q;
}else{
int nq=++stot;
len[nq]=len[p]+1;
fa[nq]=fa[q];
memcpy(nxt[nq],nxt[q],sizeof(nxt[q]));
fa[q]=fa[cur]=nq;
while(p&&nxt[p][c]==q){
nxt[p][c]=nq;
p=fa[p];
}
}
}
lst=cur;
}
void initpre(){
for(int i=1;i<=stot;i++) pre[0][i]=fa[i];
for(int i=1;i<=30;i++){
for(int j=2;j<=stot;j++){
pre[i][j]=pre[i-1][pre[i-1][j]];
}
}
}
}sam;
bool cmp(int x,int y){
if(sam.len[x]==sam.len[y]){
return isa[x]>isa[y];
}
return sam.len[x]>sam.len[y];
}
void init(){
sam.init();
for(int i=1;i<=tot;i++) in[i]=dis[i]=isa[i]=pos[i]=0,g[i].clear(),adj[i].clear();
ans=0;
}
int toposort(){
queue<int> q;
for(int i=1;i<=tot;i++) if(!in[i]) q.push(i);
while(!q.empty()){
int u=q.front();
q.pop();
ans=max(ans,1ll*dis[u]+sam.len[u]);
for(auto v:adj[u]){
dis[v]=max(dis[v],dis[u]+sam.len[u]);
in[v]--;
if(!in[v]){
q.push(v);
}
}
}
bool flag=0;
for(int i=1;i<=tot;i++){
if(in[i]) flag=1;
}
if(flag) return -1;
return ans;
}
void solve(){
init();
cin>>s;
n=s.length();
s=" "+s;
for(int i=n;i>=1;i--){
sam.expand(s[i]-'a');
pos[i]=sam.lst;
}
sam.initpre();
cin>>na;
tot=sam.stot;
for(int i=1;i<=na;i++){
int l,r;
cin>>l>>r;
int lenn=r-l+1,p=pos[r];
for(int i=30;i>=0;i--){
if(pre[i][p]&&sam.len[pre[i][p]]>=lenn) p=pre[i][p];
}
isa[++tot]=1;
sam.len[tot]=lenn;
g[p].push_back(tot);
a[i]=tot;
}
cin>>nb;
for(int i=1;i<=nb;i++){
int l,r;
cin>>l>>r;
int lenn=r-l+1,p=pos[l];
for(int i=30;i>=0;i--){
if(pre[i][p]&&sam.len[pre[i][p]]>=lenn) p=pre[i][p];
}
isa[++tot]=0;
sam.len[tot]=lenn;
g[p].push_back(tot);
b[i]=tot;
}
for(int i=2;i<=sam.stot;i++) sort(g[i].begin(),g[i].end(),cmp);
for(int i=1;i<=sam.stot;i++){
int lst=i;
for(int j=g[i].size()-1;j>=0;j--){
adj[lst].push_back(g[i][j]);
in[g[i][j]]++;
if(!isa[g[i][j]]) lst=g[i][j];
}
last[i]=lst;
}
for(int i=2;i<=sam.stot;i++){
adj[last[fa[i]]].push_back(i);
in[i]++;
}
for(int i=1;i<=tot;i++){
if(!isa[i]) sam.len[i]=0;
}
cin>>m;
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
adj[a[x]].push_back(b[y]);
in[b[y]]++;
}
cout<<toposort()<<'\n';
}
signed main(){
int T;
cin>>T;
while(T--){
solve();
}
return 0;
}
4. 倍增优化建图
区间向区间连边,可以转化为区间向虚点连边,再由虚点向区间连边。
和线段树建图极其相似,但是不同的是我们这里搬到了书上,我们同样要建出两个树,一个是出边树,一个是入边树,让后我们通过倍增求 LCA 的方法来建立:
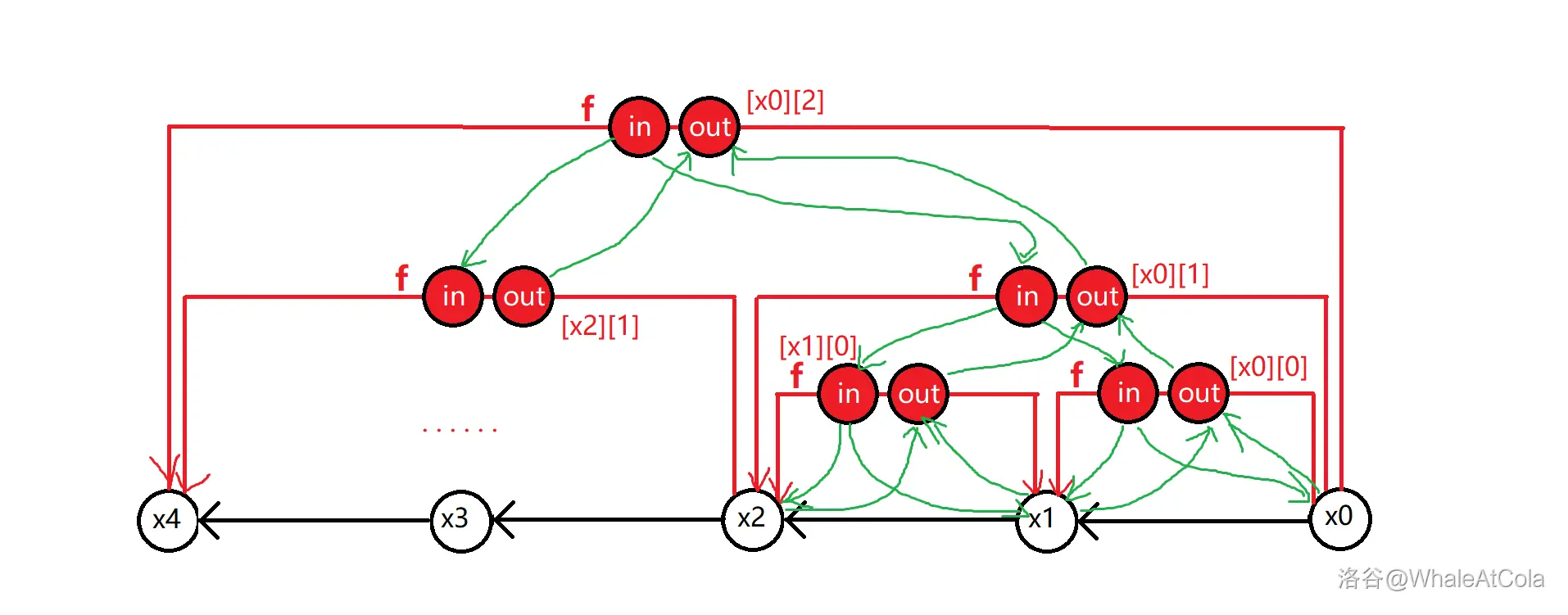
每一次我们让 [u_1,v_{1}] \to [u_{2},v_{2}] 连边时,两个跳 LCA,[u_{1},v_{1}] \to out_{[u_{1},v_{1}]},[u_{2},v_{2}] \to in_{[u_{2},v_{2}]}。让后 out_{[u_1,v_{1]}\to}in_{[u_{2},v_{2}]}。
时间复杂度在 O(n \log^2 n)。
#include<bits/stdc++.h>
#define pir pair<int,int>
using namespace std;
constexpr int MN=1e7+15;
constexpr int INF=0x3f3f3f3f;
struct Query{
int u1,v1,u2,v2,w;
}qry[MN];
int n,m,st,qtot,dis[MN],pre[MN];
bool vis[MN];
vector<pir> adj[MN],g[MN];
namespace Tree{
int dep[MN],fa[MN][20],dtot;
int in[MN][20],out[MN][20];
void dfs(int u,int pre){
dep[u]=dep[pre]+1;
fa[u][0]=pre;
in[u][0]=++dtot;
adj[dtot].push_back({u,0});
adj[dtot].push_back({pre,0});
out[u][0]=++dtot;
adj[u].push_back({dtot,0});
adj[pre].push_back({dtot,0});
for(int j=0;j<__lg(n);j++){
fa[u][j+1]=fa[fa[u][j]][j];
in[u][j+1]=++dtot;
adj[dtot].push_back({in[u][j],0});
adj[dtot].push_back({in[fa[u][j]][j],0});
out[u][j+1]=++dtot;
adj[out[u][j]].push_back({dtot,0});
adj[out[fa[u][j]][j]].push_back({dtot,0});
}
for(auto e:g[u]){
int v=e.first;
if(v==pre) continue;
dfs(v,u);
}
}
void lca1(int x,int y,int k){
if(dep[x]<dep[y]) swap(x,y);
adj[y].push_back({k,0});
for(int i=__lg(n);i>=0;i--){
if(dep[fa[x][i]]>=dep[y]){
adj[out[x][i]].push_back({k,0});
x=fa[x][i];
}
}
if(x==y) return;
for(int i=__lg(n);i>=0;i--){
if(fa[x][i]!=fa[y][i]){
adj[out[x][i]].push_back({k,0});
adj[out[y][i]].push_back({k,0});
x=fa[x][i];
y=fa[y][i];
}
}
adj[out[x][0]].push_back({k,0});
}
void lca2(int x,int y,int k){
if(dep[x]<dep[y]) swap(x,y);
adj[k].push_back({y,0});
for(int i=__lg(n);i>=0;i--){
if(dep[fa[x][i]]>=dep[y]){
adj[k].push_back({in[x][i],0});
x=fa[x][i];
}
}
if(x==y) return;
for(int i=__lg(n);i>=0;i--){
if(fa[x][i]!=fa[y][i]){
adj[k].push_back({in[x][i],0});
adj[k].push_back({in[y][i],0});
x=fa[x][i];
y=fa[y][i];
}
}
adj[k].push_back({in[x][0],0});
}
}using namespace Tree;
int root(int x){
return pre[x]==x?x:pre[x]=root(pre[x]);
}
void dijk(int st){
priority_queue<pir,vector<pir>,greater<pir>> q;
memset(dis,0x3f,sizeof(dis));
dis[st]=0;
q.push({0,st});
while(!q.empty()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(auto e:adj[u]){
int v=e.first,w=e.second;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
q.push({dis[v],v});
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>st;
dtot=n;
for(int i=1;i<=n;i++) pre[i]=i;
while(m--){
int op,u1,v1,u2,v2,w;
cin>>op;
if(op==1){
cin>>u1>>v1>>u2>>v2>>w;
if(root(u1)!=root(v1)||root(u2)!=root(v2)) continue;
qry[++qtot]={u1,v1,u2,v2,w};
}else{
cin>>u1>>v1>>w;
int ru=root(u1),rv=root(v1);
if(ru==rv) continue;
g[u1].push_back({v1,w});
g[v1].push_back({u1,w});
adj[u1].push_back({v1,w});
adj[v1].push_back({u1,w});
pre[rv]=ru;
}
}
for(int i=1;i<=n;i++)
if(!dep[i]) dfs(i,0);
for(int i=1;i<=qtot;i++){
lca1(qry[i].u1,qry[i].v1,++dtot);
lca2(qry[i].u2,qry[i].v2,++dtot);
adj[dtot-1].push_back({dtot,qry[i].w});
}
dijk(st);
for(int i=1;i<=n;i++)
cout<<(dis[i]==INF?-1:dis[i])<<" ";
return 0;
}
5. 虚点连边
区间向区间连边,可以转化为区间向虚点连边,再由虚点向区间连边。
这个话还是比较管用的,这样复杂度可以大大降低。
但是我题丢了,所以只能放一句话 www。
.png)