集训的时候讲了一下,觉得很有意思,难度也比较小,学 SA 学累了,加上感觉没太多人写这个,故有了这篇笔记。
请注意,本文所有的字符串的下标都是从 1 开始的,本人讨厌从 0 开始。
请注意,本文所有的字符串的下标都是从 1 开始的,本人讨厌从 0 开始。
请注意,本文所有的字符串的下标都是从 1 开始的,本人讨厌从 0 开始。
重要的话说三遍。
介绍
扩展 KMP 听起来像是和 KMP 有很大联系,其实他们一点关系都没有,反倒和 Manacher 的思想差不多,这个东西也叫 Z 函数,顾名思义,这个算法就是在求一个函数。
我们定义的一个函数 z[i],这个函数表示对于整个字符串和从 i 开始向后截取的字符串,两个字符串的最长公共前缀的长度。
举个例子:我们有个字符串 abbaabbca。
z[5]=3,因为显然最长公共前缀是 abb。
我们管这个叫 LCP。
我们需要做的就是在 O(n) 求出来每个位置的函数值。
所以往后本文会同时使用 Z 函数与扩展 KMP 两个名字,前者就指这个函数。
算法流程
似乎不太好做,考虑从左往右求解。
我们发现如果之前有一个最长公共前缀覆盖了我们正在求的位置,我们似乎可以继承曾经的值诶。
我们决定顺着这个思路去想。
画一个图先感性看一下,之后再去分析细节。
建议读图顺序:黄绿蓝红。
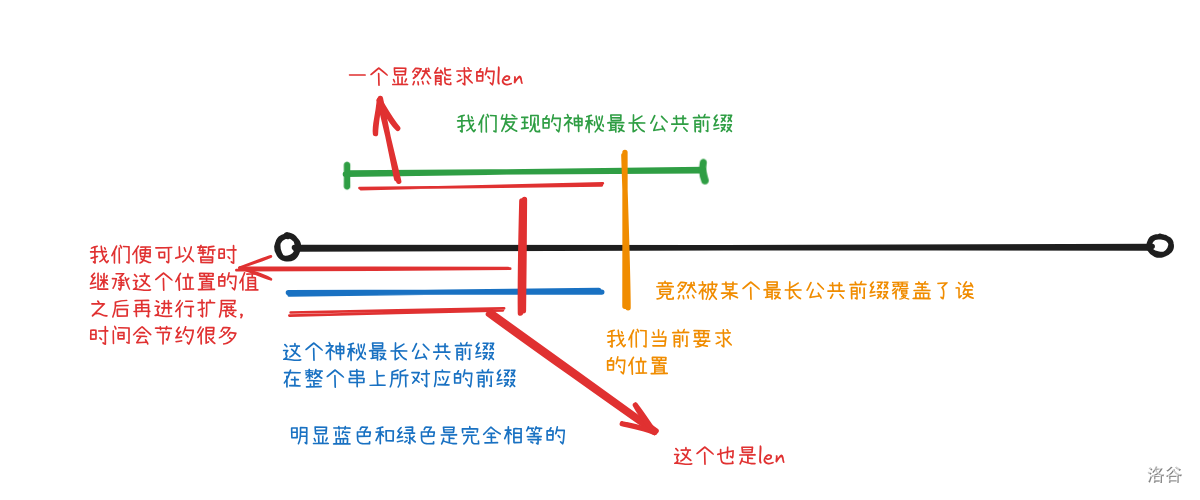
如果有一个我们维护的最长公共前缀覆盖了我们当前要求的点,我们就可以通过所记录这个最长公共前缀的起点和终点推算出我们可以继承前边已经求过的哪个点了。
按着这个思路我们来设计一下算法。
我们一共有三个步骤:继承,扩展,维护盒子。
我们管我们维护的,前边出现的最长公共前缀叫做加速盒子,因为我们是依据它才能加速我们的求解的。
请记住我们名称的转变。
所以我之后就管这个叫盒子了。
我们在外部维护两个变量 l 和 r,它们表示盒子的左端点和右端点。
继承
首先我们需要考虑的就是继承的问题,想上图一样继承前边的值来加速。
假设我们现在求的位置为 i,按照我们上边图片的思路,如果这个点被我们的盒子覆盖了,我们该继承哪一个呢?
先把上图的 len 求出来,明显就是 i-l+1。
那么我们就继承 z[i-l+1] 的值。
但这样还有一个问题,那就是我们不能保证我们继承的值完全合法。
我们仅仅可以保证盒子内是一样的,但是盒子外是未知的,这个盒子不一定完全记录了 i-l+1 的信息,中途可能更新了别的信息。
所以如果这个继承的点的值过大超出了我们盒子的范围,我们就没有办法保证正确了。
解决办法很简单,我们给这个点可能的最大值限制成它到右端点的距离就行了,保证不会超出。
人话:对 r-i+1 取 min。
所以我们对于继承的式子就出来了,如果 i\le r 的话:z[i]=min(z[i-l+1],r-i+1)。
一定不要忘记判断 i\le r,我有的时候打代码打爽了比较快会忘了这个判断。
扩展
所谓扩展,就是暴力扩展。
没有开玩笑,就是一个一个跳。
n 代表整个字符串长度,同时 s 代表字符串。
在保证 i+z[i]\le n 的情况下,我们使用一个循环判断 s[i+z[i]]=s[1+z[i]] 是否成立,也就是暴力。
每次成立我们直接将 z[i] 加一就行了。
为什么是对的我们之后再讲。
维护盒子
现在我们的 z[i] 是没有参杂一点水分的,最终形态的 z[i] 了。
但是吃水不忘挖井人,我们需要时刻维护盒子,让后边的位置享受到加速盒子的美好。
也很简单,我们判断以下当前最长公共前缀有没有延伸出盒子,前边不是暴力扩展了吗,如果伸出来了,我们将盒子左端设为当前位置,右端点设为所延伸的地方。
形式化一些,如果我们发现 i+z[i]-1 > r,我们就直接将 l 设为 i,r 设为 i+z[i]-1。
于是就没有了,你听懂了嘛。
时间复杂度
没学过 Manacher 的就会问了:主播主播,你的算法确实很强,但凭什么说这个就是 O(n) 的?这不也有暴力吗?
BaiBaiShaFeng 会告诉他这个绝对不是瞎说的。
我们会发现整个过程中 r 都是单调不减的。
而我们在 r 以内的都可以直接转移过来,而 r 最多跳 n 次。
所以是 O(n) 的。
如果还是不明白?
想象以下你正在写 n 道题,中途随时可能需要回 npy 的 n 条消息,你最后会操作 2n 次,这下就明显了吧。
代码
都说到这个份上了,随便放一下应该都能看懂了吧。
void Z_func(string s){
int n=s.size()-1; z[1]=n;//设置初始值
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);//继承
while(i+z[i]<=n&&s[i+z[i]]==s[1+z[i]]) ++z[i];//扩展
if(i+z[i]-1>r){
l=i; r=i+z[i]-1;//维护盒子
}
}
}
例题
P5410 【模板】扩展 KMP/exKMP(Z 函数)
给你两个字符串,分别是 a 和 b。我们首先要求出来 b 的 Z 函数,然后求出来 b 和 a 的每个后缀的 LCP。
需要 O(n) 的时间复杂度。
最后有输出格式要求,我们这里忽略不计了。
问题一很好求,就是之前的那个,我们思考以下怎么求问题二。
这个其实利用 Z 函数就行了。
我们将 a 拼接到 b 的右边,在两个串中间加入一个特殊符号做分割,我们在这个串上再做一次扩展 KMP。
统计的时候,我们在 b 的范围中统计,看一下在 a 中对应哪个位置,也就是 m+2+i-1,别忘了中间还有一个分割符号,得到 z[n+2+i-1],再对 m 取 min 保证能被放到 b 中就行了。
放一下代码↓
#include <bits/stdc++.h>
using namespace std;
const int MN=4e7+217;
int zb[MN], zc[MN];
void Z_funcb(string s){
int n=s.size()-1; zb[1]=n;
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) zb[i]=min(r-i+1,zb[i-l+1]);
while(i+zb[i]<=n&&s[i+zb[i]]==s[1+zb[i]]) ++zb[i];
if(i+zb[i]-1>r){
l=i; r=i+zb[i]-1;
}
}
}
void Z_funcc(string s){
int n=s.size()-1; zc[1]=n;
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) zc[i]=min(r-i+1,zc[i-l+1]);
while(i+zc[i]<=n&&s[i+zc[i]]==s[1+zc[i]]) ++zc[i];
if(i+zc[i]-1>r){
l=i; r=i+zc[i]-1;
}
}
}
string a, b, s;
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>a>>b; int n=a.size(), m=b.size(); a=' '+a; b=' '+b;
s=" "+b.substr(1)+"|"+a.substr(1); Z_funcb(b); Z_funcc(s);
long long res=0;
for(int i=1; i<=m; ++i) res^=(long long)1*(i)*(zb[i]+1);
long long ans=0;
for(int i=1; i<=n; ++i){
int p=zc[m+2+i-1]; p=min(p,m);
ans^=(long long)1*(i)*(p+1);
}
cout<<res<<'\n'<<ans<<'\n';
return 0;
}
CF432D Prefixes and Suffixes
给你一个字符串 s,定义一个完美子串为一个同时是 s 的前缀和后缀的子串,需要统计有几个这样的子串并统计每个在这个串中的出现次数。
这里的 \left | s\right | \le 10^5。
我们发现统计有几个这样的子串是很简单的,只需要使用 KMP 的 nxt 数组,从 nxt[n] 开始不停跳 nxt 就行了。
来学这个的想必都对 KMP 这种基础一些的东西很了解了。
我们其实只需要统计一定长度的前缀在串中出现了多少次。
这个东西是可以使用扩展 KMP 做的,我们维护每个长度的前缀在串中出现的次数,对于位置 i,我们将它视为一个子串的左端点,发现它可以贡献 [1,z[i]] 长度的前缀数量,我们直接将这个区间的数量加一就行。
这个可以 O(n) 差分的,但是我喜欢树状数组,反正数据范围小,具体维护无所谓啦。
代码↓
#include <bits/stdc++.h>
using namespace std;
const int MN=1e6+116;
string s; int n, z[MN], nxt[MN];
struct BIT{
int tr[MN], n;
void init(int _n){
n=_n; memset(tr,0,sizeof(tr));
}
int lowbit(int x){
return x&(-x);
}
void update(int pos, int val){
for(int i=pos; i<=n; i+=lowbit(i)) tr[i]+=val;
}
void update_range(int l, int r, int val){
update(l,val); update(r+1,-val);
}
int qval(int pos){
int res=0; for(int i=pos; i; i-=lowbit(i)) res+=tr[i];
return res;
}
}bit;
vector <pair<int,int>> qry;
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>s; n=s.size(); s=' '+s; z[1]=n; bit.init(n);
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
while(i+z[i]<=n&&s[i+z[i]]==s[1+z[i]]) ++z[i];
if(i+z[i]-1>r){l=i; r=i+z[i]-1;}
}
int j=0; nxt[1]=0;
for(int i=2; i<=n; ++i){
while(j&&s[j+1]!=s[i]) j=nxt[j];
if(s[j+1]==s[i]) j++; nxt[i]=j;
}
for(int i=2; i<=n; ++i){
if(z[i]) bit.update_range(1,z[i],1);
}
int pos=n;
while(pos>0){
qry.push_back({pos,bit.qval(pos)+1});
pos=nxt[pos];
}
reverse(qry.begin(),qry.end());
cout<<qry.size()<<'\n';
for(auto v:qry){
cout<<v.first<<" "<<v.second<<'\n';
}
return 0;
}
一些扩展 KMP 也可以干的事情
这里收回我之前说的话,其实两个算法还是有共同点的,有一些 KMP 可以干的事情我们的扩展 KMP 同样可以干,个人认为这一块没什么大用,能用 KMP 为啥不用,但对于掌握扩展 KMP 还是有一定用途的,再说了 OI Wiki 都放了。
匹配子串
这是 KMP 可以做的那个模式串与文本串的匹配,我们只能搞最长公共前缀,想要匹配怎么办。
这个简单,我们把模式串拼到文本串之前,再向中间加一个特殊的分隔符,这样再跑扩展 KMP,我们会发现在这上边我们就可以匹配了。
我们只需要看看后边属于文本串的函数值有没有达到模式串的长度,这个正确性是比较好想的,我就不展开讲了,实在不懂画个图。
下边是 A 掉 KMP 模板的代码,匹配子串不需要 nxt 数组,只是题目需要输出 nxt 数组而已。
代码↓
#include <bits/stdc++.h>
using namespace std;
const int MN=2e7+117;
string s, t, str;
int z[MN], n, nxt[MN];
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>s>>t; str=t+'#'+s; n=str.size();
str=' '+str; z[1]=n;
for(int i=2,l=1,r=1; i<=n; ++i){
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
while(i+z[i]<=n&&str[i+z[i]]==str[1+z[i]]) ++z[i];
if(i+z[i]-1>r){l=i; r=i+z[i]-1;}
}
int m=t.size(), j=0; t=' '+t; nxt[1]=0;
for(int i=2; i<=m; ++i){
while(j&&t[j+1]!=t[i]) j=nxt[j];
if(t[j+1]==t[i]) ++j;
nxt[i]=j;
}
for(int i=m+1; i<=n; ++i){
if(z[i]==m){
cout<<i-m-1<<'\n';
}
}
for(int i=1; i<=m; ++i) cout<<nxt[i]<<" ";
}
本质不同子串数量
这个应该可以使用 SA 或者 SAM, 都可以 O(n) 来做,而如果使用 Z 函数就是 O(n^2) 的,所以这个大概没什么用,不给代码了。
考虑已经知道了串 s 的本质不同的子串数量,现在插入一个字符,计算数量的变化情况。
我们可以将 s 与后边加上的字符看作串 s',对 s' 进行一下翻转,我们对这个 s' 去求 Z 函数。
我们将这个问题转化为了一个前缀的问题,我们新增了一些以新字符打头的前缀,现在我们想知道在整个串中有多少串是没有出现过的。
这个并不难做,我们找出跑出来的 Z 函数的最大值,这个就是在串中出现过的最长前缀,同时说明比它小的前缀同样出现了。
所以每次的贡献就是 \left | s'\right |-z_{max}。
于是我们就会做了。
如果问题改为在端点添加或者删除一个字符,让你统计我们就是 O(n) 的了,万一用得上呢。
求解字符串整周期
就是找一个最小的字符串 t,使得整个串被这个 t 所拼接表示。
没错,这个就是能 KMP 做,但是我们现在要使用今天的东西。
我们直接寻找最小的 i 满足 i+z[i]=n。
直观的,对于满足这样的一个 i,它的前缀是 n-i,也就是可以覆盖整个字符串,正确性同 KMP 的证明。
需要特别注意:如果要求整周期,需要保证 i 是 n 的因数,而如果只是求解最短循环节就不需要这个限制。
结语
写了这么久也累了,总结以下这片笔记的内容吧。
扩展 KMP,又称 Z 函数,是一个直接用于解决最长公共前缀的字符串算法,衍生出一些用法,与 KMP 有重叠,但对于各点与整串的前缀处理方面有独到的作用。
这个算法的题目还是比较少的,所以没有太多的例题,我做过的除例题外的这类题都放到下边了。
本文参考了 OI-Wiki,主要参考了扩展 KMP 的应用,也是为了更好的总结。
如果本文有任何的问题,错误,不足或者模糊的地方,欢迎各位进行指正,如果有好的题目也可以分享一下,如果有空会将一些好题加入这篇文章。
最后的,祝福大家 OI 学习开心,也纪念本人学习 OI 的一周年。
一些题目
CF1968G2 Division + LCP (hard version)
.png)
