Logo

Menu

搜索杂谈

starlinkOvO
Published on 2025-05-25 / 11 Visits
0
0
#笔记#搜索

写在前面

针对能力全面提升综合题单Part3 搜索中的题目及对应知识点的总结，但是以后半部分为主（当然我主次不分就是了）。

而且深受某网站八股文的影响

目录

  1. 记忆化搜索 & 剪枝
  2. 折半搜索（meet in middle）
  3. 双向搜索
  4. A* 算法
  5. IDA* 算法

原来是有跳转的但是好像不能用我也不修了，就这么凑合看吧。

参考文章

【BZOJ4800】[CEOI2015 Day2]世界冰球锦标赛 （折半搜索）

一个国外网站关于折半搜索(Meet in the middle)和双向搜索(Bidirectional Search)的介绍。

记忆化搜索 & 剪枝

有时，当我们信心满满的写好了代码，兴致勃勃的提交，然后 T 飞了！

这时候就可以试试记忆化 or 剪枝了。

记忆化

对于某些题，我们发现在搜索的过程中可能会有一些数据被搜索到，这样就占用了许多的时间。

但是如果我们能够开一个数组，将那些搜索结果记录下来，在遍历到这个数据时直接返回，就能节省很多时间！

假如要求斐波那契数列，我们对每个数都求解一遍是很麻烦的。
但是众所周知，斐波那契数列是可以通过上一个数字的值推出下一个值，这样就很方便，同时也很迅速。
记忆化搜索就是这个思路。

例题：P1434 [SHOI2002] 滑雪

先考虑暴力，枚举起点，DFS 出其最长路径，最后取每次搜索的最大值。

但是我们发现每一个点向下能走的最长路径都是固定的，于是考虑记忆化，将每个点向下的最长路径存下来，DFS 到了就直接返回。

若该起点没有被记录，该点向下的最长路径就是其下第一个点的最长路径加 1，DFS 下去就好。

代码直接在 DFS 板子的基础上改，非常简单。

核心代码如下：

int dfs(int x, int y) {
    if (f[x][y]) return f[x][y];

    f[x][y] = 1;

    for (int i = 1; i <= 4; i++) {
        int tx = x + dx[i], ty = y + dy[i];
        if (tx > r || ty > c || tx < 1 || ty < 1 || mp[tx][ty] <= mp[x][y]) continue;

        f[x][y] = max(dfs(tx, ty) + 1, f[x][y]);
    }

    return f[x][y];
}

剪枝

我们发现，搜索时会搜到很多种情况，但是最终答案可能只有一种，也就是说，搜索过程中搜到了许多没有意义的答案，若我们能在搜索开始前跳过一些情况，更加快速地找到答案。
这就是剪枝。

个人认为，剪枝可以很简单也可以很难，有的时候你随手打的 if (tim > maxn) return; 就是剪枝，但是有的剪枝想一整天还是 T 的飞起。。。

例题：P1120 小木棍

经典中的经典。

但是最近没写先咕咕咕~

折半搜索（meet in middle）

关于折半搜索的一点碎碎念。

顾名思义，就是将原有数据分成两份进行搜索，最后在中间进行答案结合。

我觉得这个和二分与分治有异曲同工之妙。

干讲不好讲，所以我们直接看题。

例题：P4799 [CEOI 2015] 世界冰球锦标赛 (Day2)

首先爆搜很好想，但是 N \leq 40，也就是说可能会有高达 O(2 ^ {40}) 的复杂度，包飞起来的。

那么考虑折半搜索。

将数据分为两部分，分别对这两部分进行搜索，当搜索到所需钱数大于上限时就返回。

在我们可以设一个区间 (l, r)，每次枚举下标为 l 的比赛是否观看，然后缩小范围直至 l \gt r 时返回。

考虑如何合并答案。我们将答案存在两个数组里，对其中一个数组排序，枚举另外一个数组中的数，每次对排序后的数组upper_bound() 寻找第一个大于总数减去枚举出的数的数，然后下标减一，直接加到 ans 里。

由于我们排好序了，所以这里其实是加上第一个不符合条件的之前的所有数的个数，就不用在一个一个加了。

由于我们是分成两份搜索的，即相当于数据减少了一半，那么时间复杂度就降低为了 O(2^{n / 2})，即最高仅有 O(2^{20})。

然后就能写出代码了（记得开 long long）。

int n, m, mid;
int w[55]; //票价
int suma[1 << 20], sumb[1 << 20]; //两个数组
int cnta, cntb, ans;

void dfs(int l, int r, int sum, int a[], int &cnt) {
    if (sum > m) return ;
    if (l > r) {
        a[++cnt] = sum;
        return ;
    }

    dfs(l + 1, r, sum + w[l], a, cnt);
    dfs(l + 1, r, sum, a, cnt);
}

signed main() {
    //输入略
    mid = n >> 1;

    dfs(1, mid, 0, suma, cnta);
    dfs(mid + 1, n, 0, sumb, cntb);

    sort(suma + 1, suma + cnta + 1);
    for (int i = 1; i <= cntb; i++)
        ans += upper_bound(suma + 1, suma + cnta + 1, m - sumb[i]) - suma - 1;
    
    //输出略
}

复杂度证明

看完了上面的内容，你可能会发出这样的疑问：

欸那为什么折半搜索的复杂度更低呢？

好问题。

网上找不到合适的图，我自己也画不出来，大家就看文字感性理解一下吧。。。

我们这样考虑：假设不用折半搜索，且不考虑其他剪枝，对于这道题相当于要枚举 2^{n} 个组合。
但是如果我们分开考虑，也就是说只需枚举 2^{n/2} 个组合来得到两个集合，显然这么做是更快的。

接下来考虑将两份答案合并起来。

一种朴素的想法是直接枚举这两个集合中的所有元素，将它们一一配对，那样时间复杂度就是 O({2^{n/2}}^{2})，即 O(2 ^ {n})，我们发现前面节省下来的时间又在这里用回来了，那么就要考虑优化。

我们假设折半搜索出来了 X 和 Y 这两个集合。

既然题目给出了最大值的限制（假设为 maxn），我们可以先对 Y 进行从小到大排序，枚举 X 中的每个元素 x，在 Y 中二分查找 y，使得有 x + y \leq maxn。

这样复杂度就从 O(2 ^ {n}) 降低至 O(2 ^ {n / 2} \cdot \log (2^{n/2}))，即 O(2 ^ {n / 2} \cdot n)，最终得到 O(2 ^ {n / 2})。

写完这个可以去写P3067 [USACO12OPEN] Balanced Cow Subsets G。

一些碎碎念

在写文章的时候，我发现我对于折半搜索和双向搜索的区别并没有非常清晰的理解，于是查阅了我认为比较大量的资料，但是发现许多人在写折半搜索是实际是上讲的是双向搜索，甚至有的直接混为一谈。

有的解释是对的，但是图片我认为是不正确的（或者不清晰？即这个和这个），我不知道别人如何看待，至少给我造成了很大的误解。

双向搜索

双向搜索，或者叫双向同时搜索更贴切一些，顾名思义，就是从起点和终点同时进行搜索，直至发现了焦点，此时就有从起点通往终点的路径。

适用于起点状态和终点状态都很明确，且操作可逆的情况，比如接下来我要说的八数码难题。

那么关于为什么这么做复杂度更低，我们可以看这两幅图（没错就是我刚刚说是错误的那两张）：

图一

上面那张表示普通的 BFS 搜索树，可以发现虽然终点状态只有一个，但是我们还是搜索出了其他的“终点”，显然这么做是很慢的。

图二

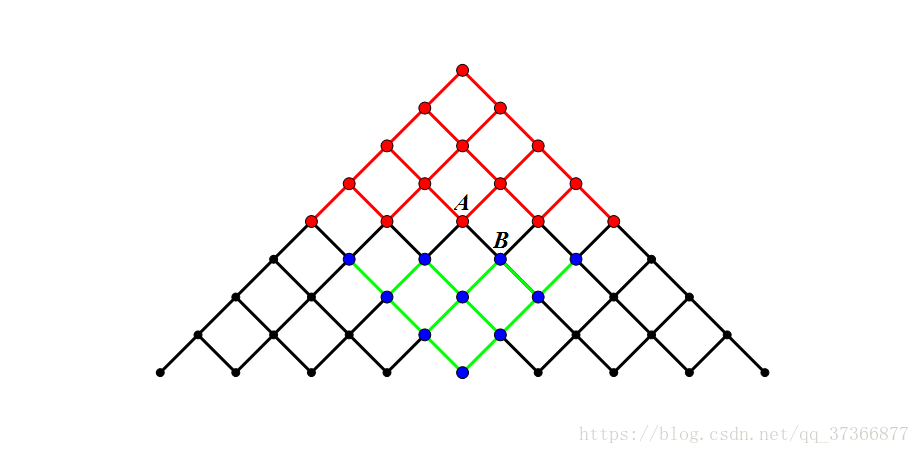
这个就是双向搜索的搜索树，可以看到原来普通的 BFS 会搜索到的一些状态使用双向搜索时不会被搜到的，这样的速度就更快了。

例题：P1379 八数码难题

不是题解里怎么全是康托展开啊，我不会啊喂。

因为直接搜索复杂度会很高（也能过），所以可以考虑双向搜索。

首先我们将初始状态和目标都压进队列里，并打上不同的标记，这样我们就能判断什么时候相遇。

然后就是正常的 BFS，但是不同的是我们要加入对相遇状态的判断。

我们将从起点搜索到的状态打上标记 1，另一个打上标记 2，当我们发现当前状态和我们枚举到的状态标记之和为 3 时说明出现了相遇，直接返回步数之和即可。

/*双向搜索*/
const int goal = 123804765;
const int dy[] = {0, -1, 1, 0}, dx[] = {-1, 0, 0, 1};
//左 上 下 右 
int n;
queue < int > q;
map < int, int > m;
map < int, int > ans;

void solve() {
    q.push(n); q.push(goal);

	m[n] = 1, m[goal] = 2;
    ans[n] = 0, ans[goal] = 1;
	while (!q.empty()){
		int t = q.front(), cur;
        cur = t;
		q.pop();
		int c[3][3], f = 0, g = 0;

		//将数字转为对应图像 
		for (int i = 2; i >= 0; i--)
			for (int j = 2; j >= 0; j--){
				c[i][j] = cur % 10;
				cur /= 10;
				if(!c[i][j]) f = i, g = j;
			}

		for (int i = 0; i < 4; i++){
			int x = f + dx[i], y = g + dy[i];
			cur = 0; //新图像的编码

			if (x < 0 || x > 2 || y < 0 || y > 2) continue;

			swap(c[x][y], c[f][g]);

			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					cur = cur *10 + c[i][j]; //更新编码

			if (m[cur] == m[t]) {
                swap(c[x][y], c[f][g]);
                continue;
            }
            else if (m[cur] + m[t] == 3) {
                cout << ans[t] + ans[cur];
                return ;
            }

            ans[cur] = ans[t] + 1;
            m[cur] = m[t];
            q.push(cur);

			swap(c[x][y], c[f][g]);//复原 
		}
	}
}

int main(){
    //...
    if (n == goal) {
        cout << 0;
        return 0;

	solve();
}

A* 算法

咕咕咕~

IDA* 算法

咕咕咕~

矩阵快速幂优化DP
欧拉函数

Comment