看了就能睡着的超绝 FHQ Treap 文章

前置

二叉搜索树 BST

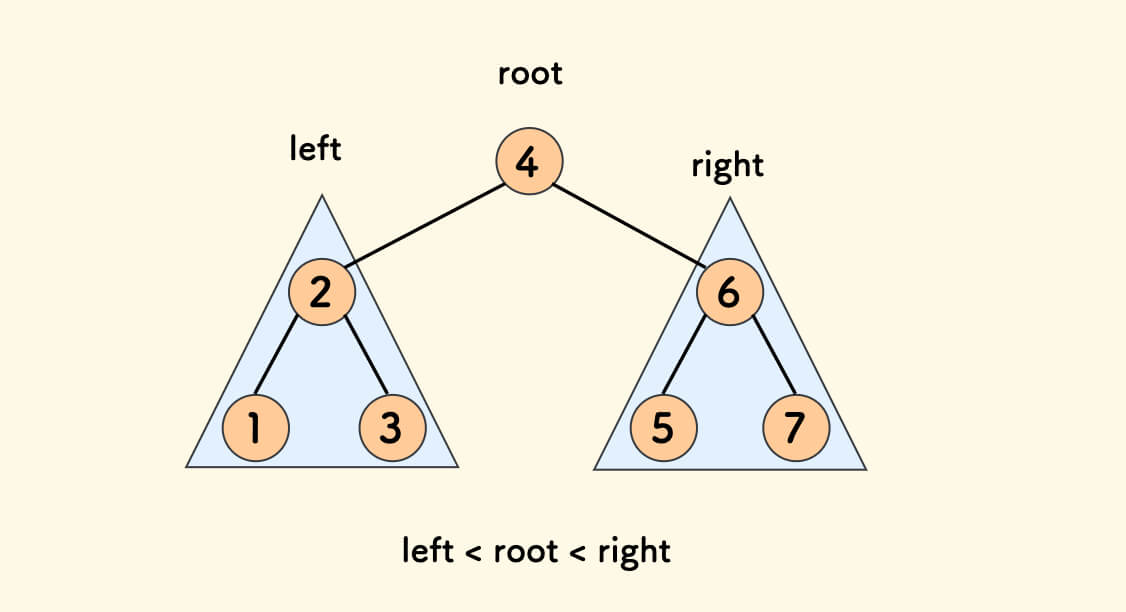
BST 有以下两个性质：

1. 二叉树
2. 节点的权值始终为 left<root<right。

堆 Heap

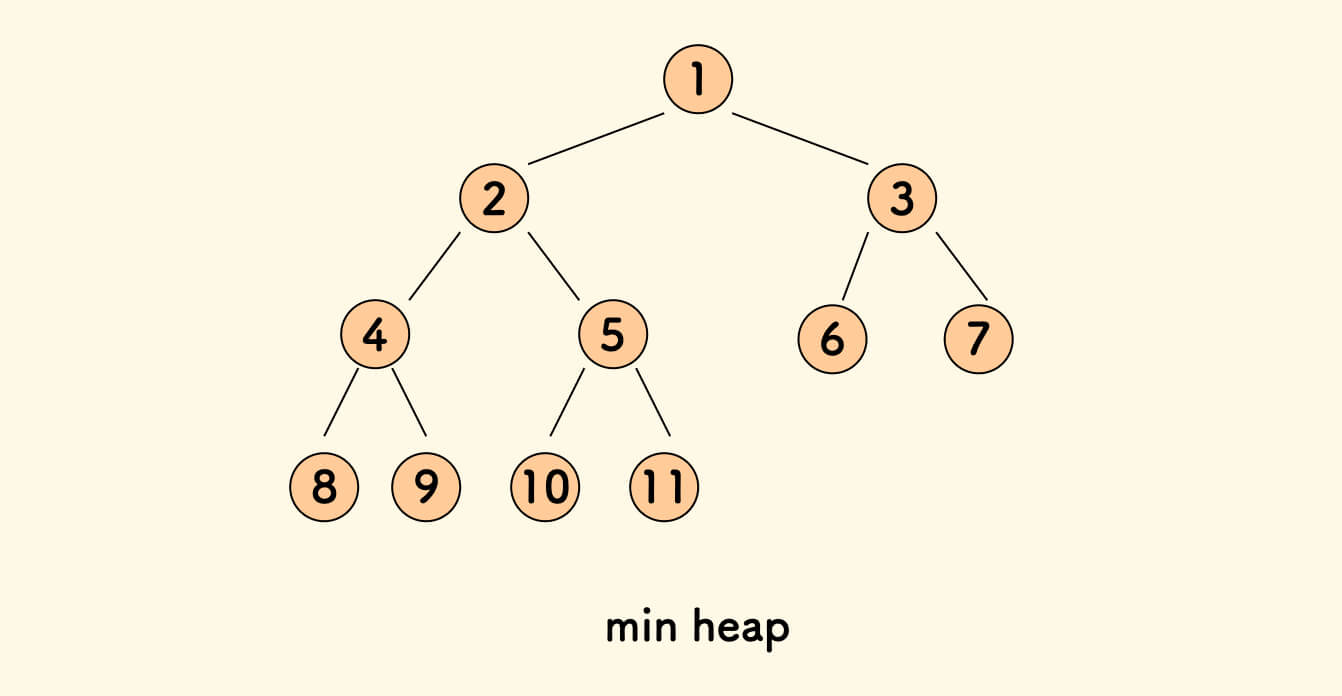
所有父亲的值都不大于两个儿子的值的完全二叉树，叫做堆。

即 root \leq left 且 root \leq right。

树堆 Treap

Treap 的节点维护两个信息：

1. 权值 val：这是维护的真正信息，其在树中形成 BST，利用 BST 的性质进行搜索。
2. 随机值 rnd：利用此值形成 Heap，以实现随机平衡（弱平衡），其期望上可以把树高控制在 \log n，因为 BST 的搜索复杂度和树高相关，其就可以避免 BST 被特殊数据卡到单次 O(n) 的复杂度。

FHQ Treap 是范浩强发明的一种无旋 Treap，其代码量小，操作方便，理解简单，且所有扩展操作都只基于两种基本操作：分裂与合并。

FHQ Treap 核心操作

结构

FHQ Treap 通过一个结构体来储存节点信息，基本的 FHQ Treap 只维护五个信息：左右儿子、权值、随机值、树的大小。

此外，还需要记录根节点。

struct Tre{
    int left,right;
    int num,sz,rnd;
}tre[MN];
int root;

pushup 函数

只维护树的大小的最基本的 pushup 函数。

void pushup(int p){
    int left=tre[p].left,right=tre[p].right;

    tre[p].sz=tre[left].sz+tre[right].sz+1;//爹的大小是俩儿子加自己
}

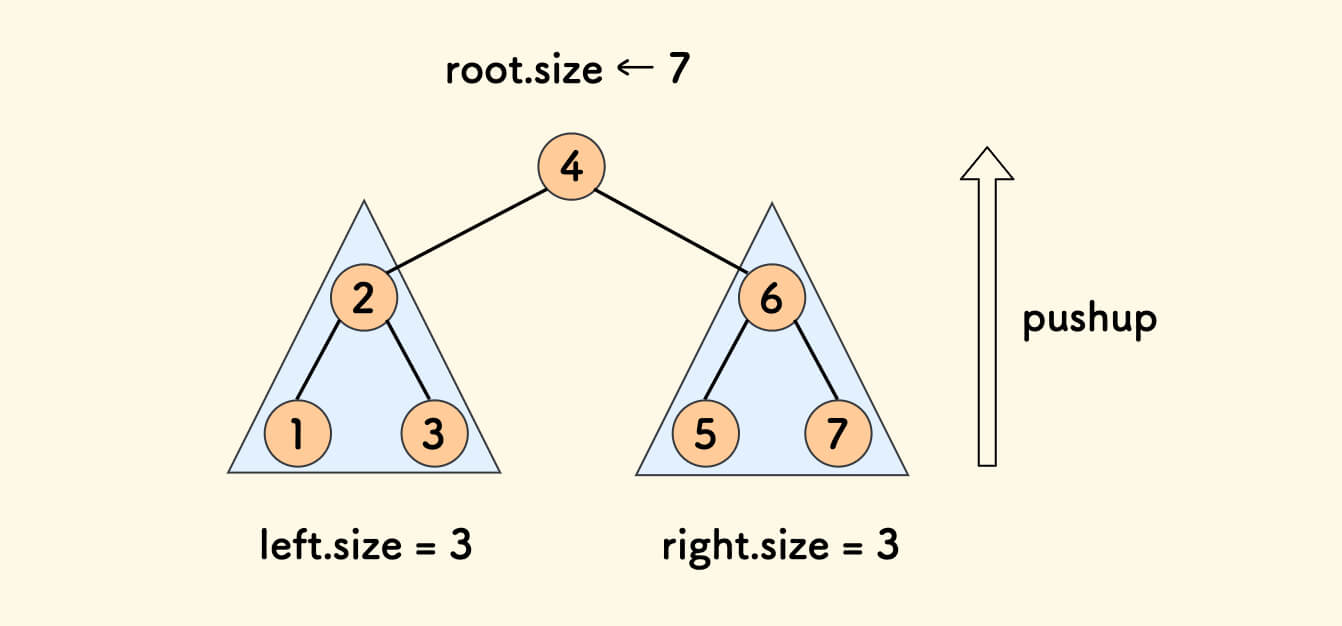
类似于线段树的 pushup 操作，它也是在其他操作完成后调用的。

分裂 split

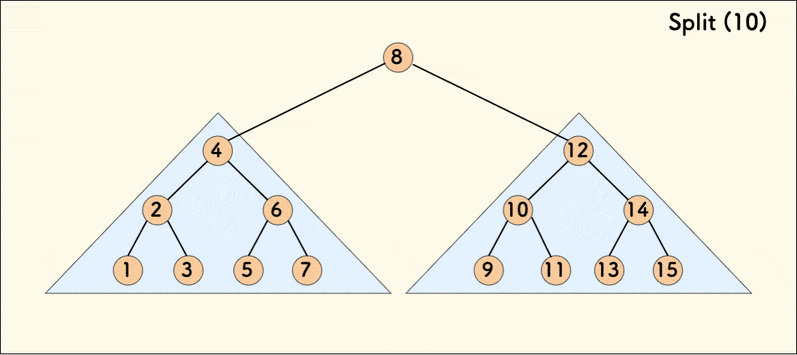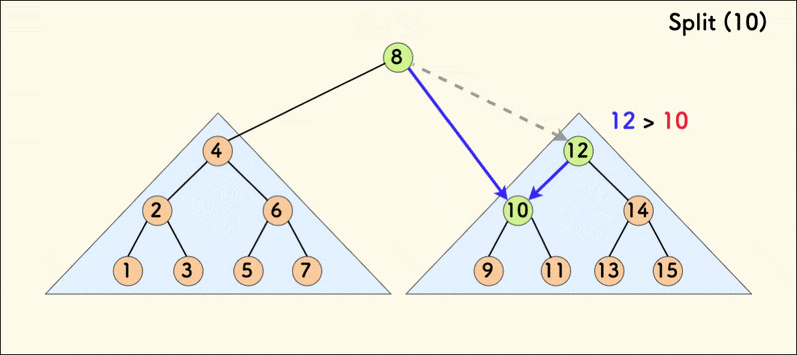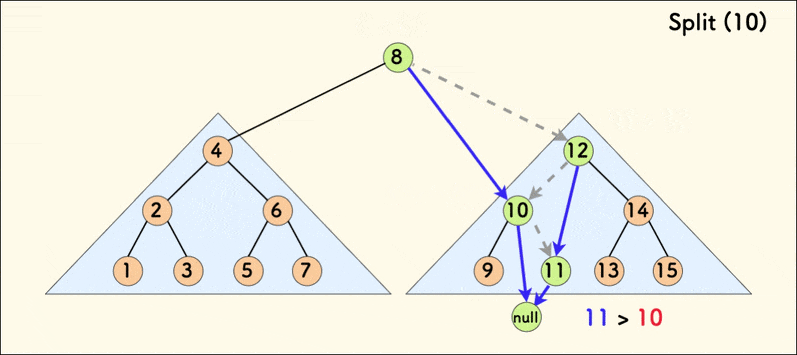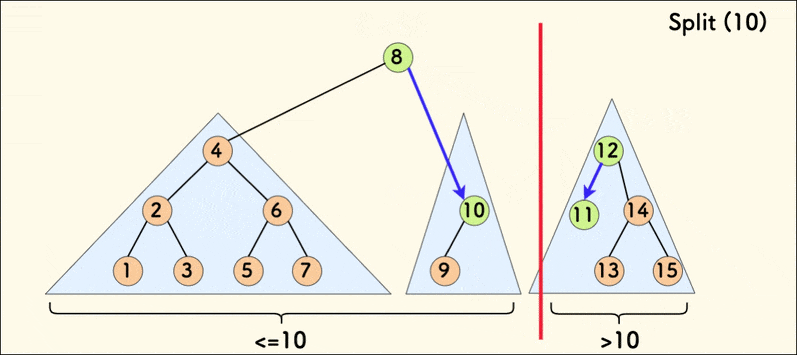
split(p,k,&x,&y) 的意思是：

• 把树 p 按照值 k 分裂成两棵子树 x 和 y，使得 x 的权值全部不大于 k，y 的权值全部大于 k。

void split(int p,int &x,int &y,int k){//定义两棵子树xy x<=k y>k 保持BST性质
    if(!p){
        x=y=0;return;
    }//如果p节点不存在，那么子树xy也不存在，返回

    if(tre[p].num<=k){//如果p节点的权值小于k，那么它本身和它的左子树都属于x 右子树属于y
        x=p;
        split(tre[p].right,tre[p].right,y,k);
    }else{
        y=p;
        split(tre[p].left,x,tre[p].left,k);
    }
    pushup(p);
}

可以看到，p 本身的权值小于等于 k 的时候，就把 p 变成自己的左子树，否则变成右子树。然后把另外一边继续 split，直到完全分裂成两棵树。这两棵树都符合 BST 的性质，且一颗中的所有权值都小于等于 k，另一颗全部大于 k。

很显然，分裂的次数就是树高，所以单次分裂操作的期望复杂度为 O(\log n)。

也很明显，分裂操作利用的是 BST 的性质，只用到了 val 而没有用到 rnd。

合并 merge

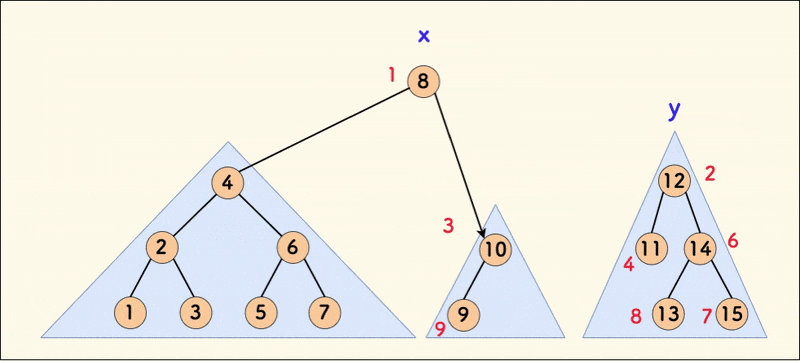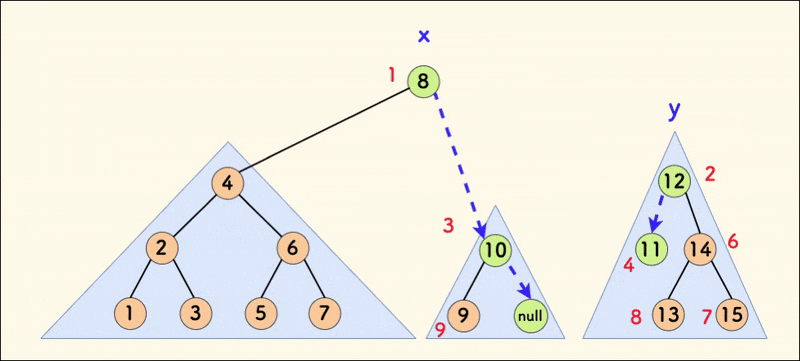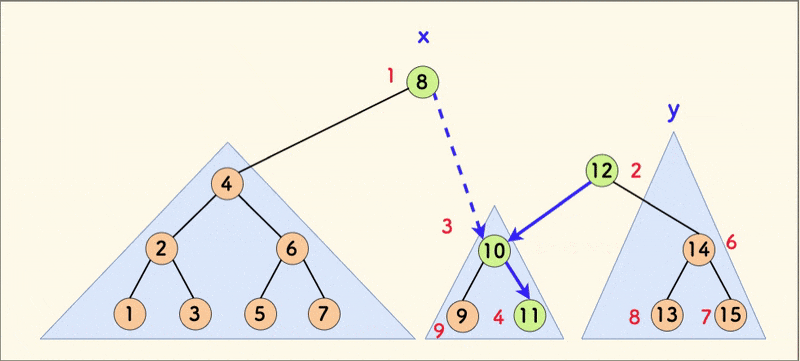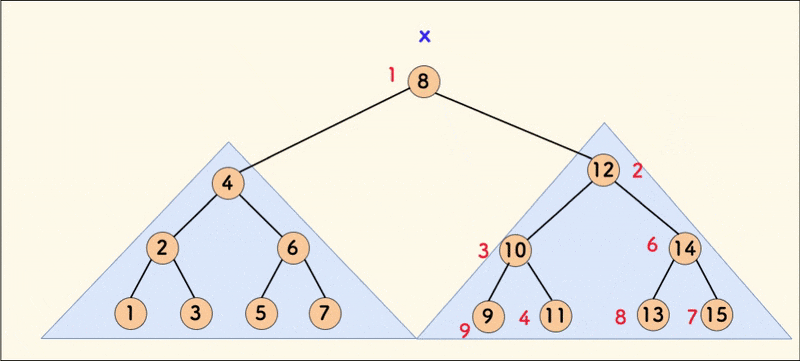
merge(x,y) 的意思是：

• 将权值较小的树 x 和权值较大的树 y 按照 rnd 的值进行合并，将 rnd 更小的点作为树根，使其成为一颗新的 FHQ Treap。

这种通过随机值进行合并的树，在数学期望上的树高是 \log n，具体证明我也不会。

int merge(int x,int y){//按照rnd的值合并xy 把rnd更小的放到上面 并返回合并后的顶点编号
    if(!x || !y) return x+y;//返回xy中那个有值的

    if(tre[x].rnd<tre[y].rnd){ //如果x的rnd比y小，那么就把它当作新的顶点合并，下面同理
        tre[x].right=merge(tre[x].right,y);
        //由于y节点中的值都比x大，为了维护左小右大的性质，需要让x的右节点和y合并
        pushup(x);//x当作新的顶点 所以pushup x
        return x;
    }else{
        tre[y].left=merge(x,tre[y].left);
        pushup(y);
        return y;
    }
    //merge会返回新的treap的根节点
}

假如此时，x 的 rnd 更小，那么就把 x 作为根节点，可以发现 y 的权值一定都比 x 大，应该和 x 的右子树合并。反之亦然。

很显然，单次合并的次数也是树高，所以单次合并的期望复杂度为 O(\log n)。

也很显然，合并利用的是 Heap 的性质，在合并过程中维护了 BST 的性质，使其不至于被破坏。

克隆 clone

Treap 使用动态开点，建立的时候随机一个 rnd 值。

int clone(int k){//建立一个权值为k的节点
    int tmp=++cnt;
    tre[tmp].num=k;
    tre[tmp].rnd=rand();
    tre[tmp].sz=1;
    return tmp;//返回节点编号
}

FHQ Treap 常用操作

插入 insert

如果你理解了上面两种基础操作的定义，那么你就能很简单的理解插入操作。

要插入一个权值为 k 的节点：

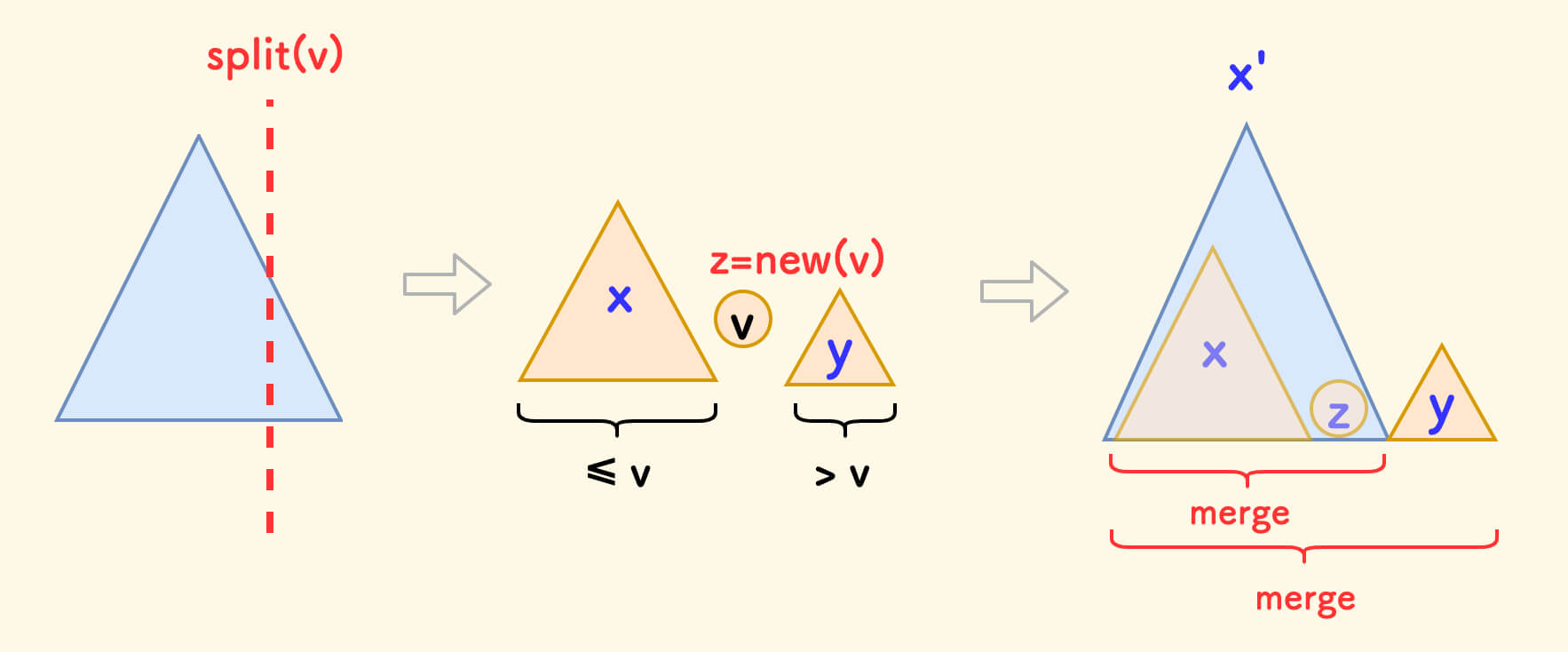
1. 以 k 为权值分裂出子树 x、y。
2. 新建一个权值为 k 的节点 z。
3. 先合并 x、z，再合并 y。

void insert(int k){
    //插入一个权值为k的点时，先以k为权值分裂treap
    //然后给权值k新建一个节点z，此时x<z<y，按顺序先合并xz，再合并y
    //注意merge函数对x，y大小有要求，需要符合传参要求
    int x,y,z;
    split(root,x,y,k);
    z=clone(k);
    root=merge(merge(x,z),y);
}

删除 erase

同上，非常简单。

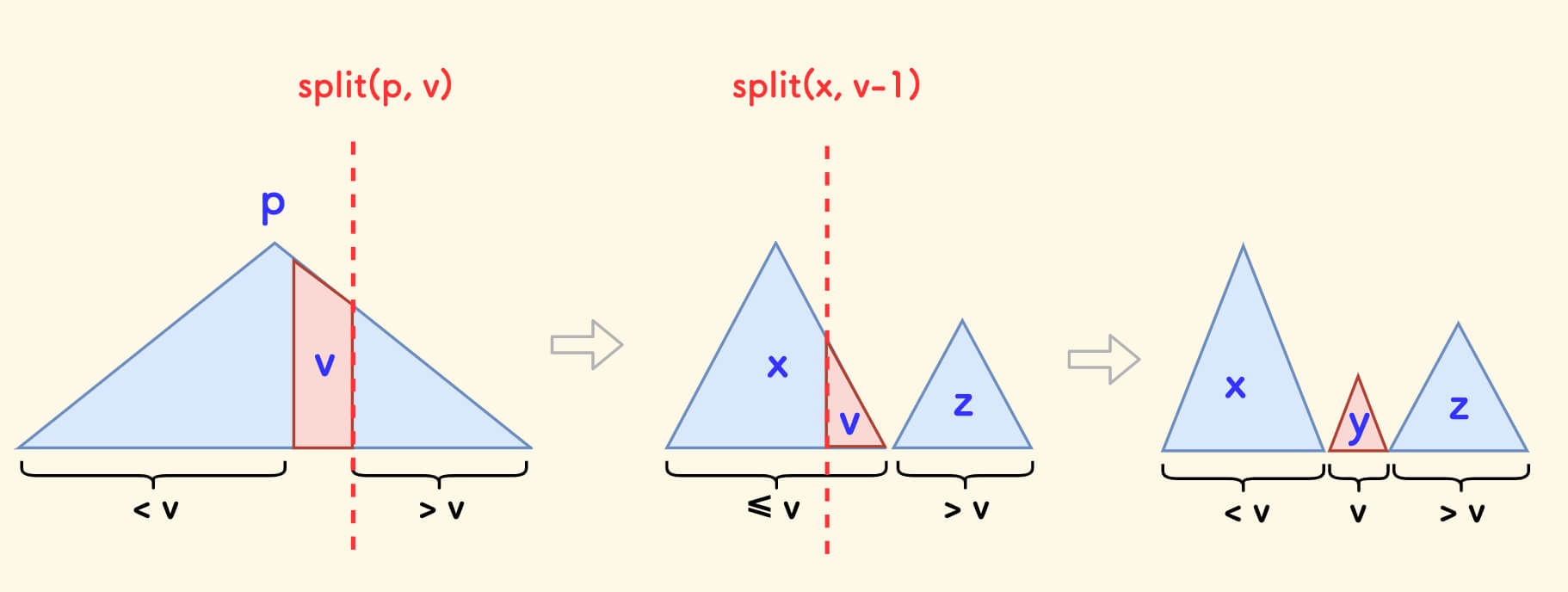
要删除权值为 k 的点：

1. 按 k 分裂出子树 x、y。
2. 按 k-1 把 x 分裂成 x、z。

此时，z 节点中是所有权值为 k 的节点。

接下来，如果只删除一个权值为 k 的点：

• 把 z 的左右子树合并，这样子就删除了 z 的根节点。然后先合并 x、z，再合并 y。

如果删除所有权值为 k 的点：

• 直接合并 x、y。

void erase(int k){
    //先按k分裂出xy
    //再按k-1分裂x,得到xz
    //此时x<=k-1，z>k-1，又因为x,z<=k 所以k-1<z<=k，即z是权值为k的点

    //此时，如果需要删除所有权值为k的点，只需要忽略z，即直接合并xy
    //如果只需要删除一个，就合并z的左右子树，相当于删去了一个z的顶点
    //然后xzy顺序合并

    int x,y,z;
    split(root,x,y,k);
    split(x,x,z,k-1);

    z=merge(tre[z].left,tre[z].right);//此处只需要删除一个
    root=merge(merge(x,z),y);
}

排名 getrank

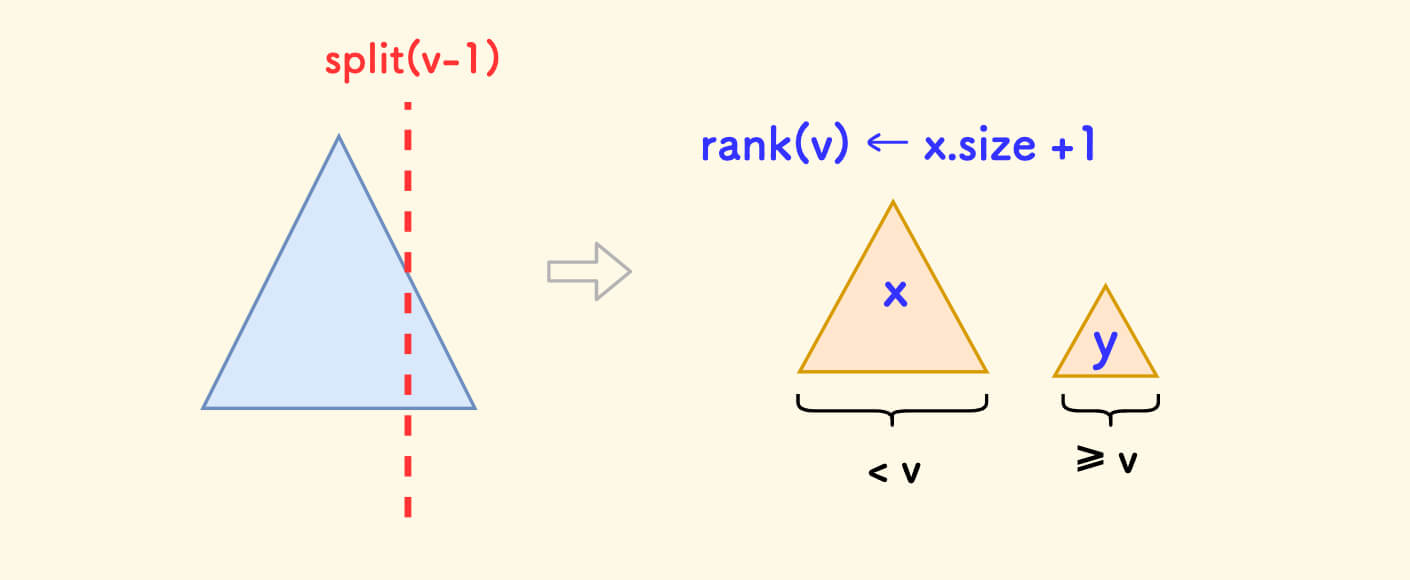
得到权值为 k 的节点在树中的排名，很明显答案为比 k 小的数的数量再加一。

1. 按 k-1 分裂出 x、y 两棵子树。
2. 记录 ans=tre[x].size+1。
3. 合并 x、y。
4. 返回 ans。

int getrank(int k){//查询权值k在树中的排名
    //只需要按k-1分裂，其左子树x的大小就是比k小的值的数量，+1就是排名
    //求完之后还需要合并回去
    int x,y,ans;
  
    split(root,x,y,k-1);
    ans=tre[x].sz+1;
    root=merge(x,y);
  
    return ans;
}

第 k 小 getkth

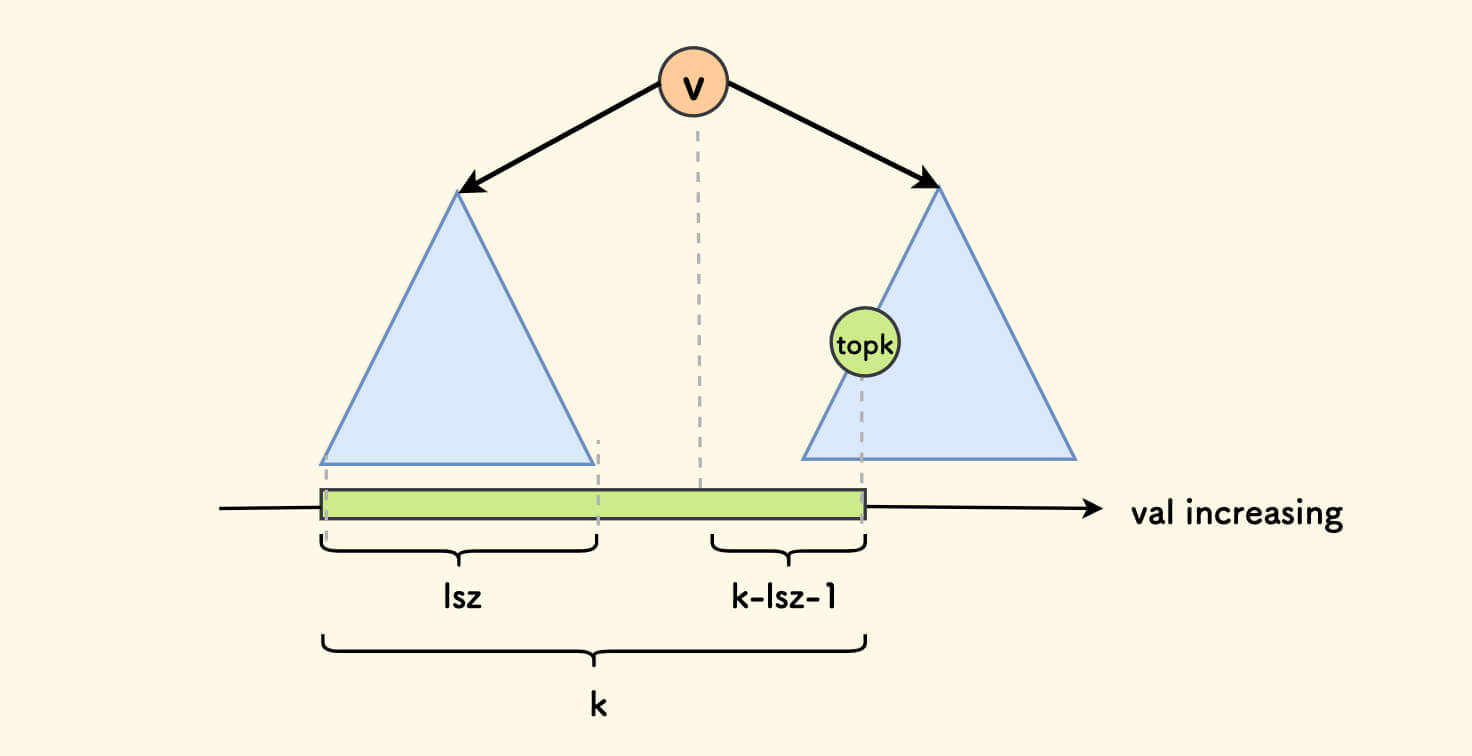
得到第 k 小的数的值。

约定左右子树大小分别为 lsz、rsz 利用 BST 的性质，分情况讨论：

1. 当 k=lsz+1 的时候，说明当前根节点就是第 k 小，直接返回根节点的权值。
2. 当 k<lsz+1 的时候，说明第 k 小在左子树中，继续询问左子树的第 k 小。
3. 当 k>lsz+1 的时候，说明第 k 小在右子树中，由于左子树和根节点的存在，所以询问右子树的第 k-lsz-1 小。

int getkth(int p,int k){//求出树中第k小的权值
    //如果k=左子树大小+1，那么节点p的值就是答案
    //如果k<左子树大小+1，那么kth在左子树中，向下递归左子树
    //如果k>左子树大小+1，那么kth在右子树中，因为左子树已经有左子树大小+1个点了
    //所以向下递归右子树的第kth-左子树-1小
    int lsz=tre[tre[p].left].sz;
    if(k==lsz+1) return tre[p].num;
    else if(k<lsz+1) return getkth(tre[p].left,k);
    else return getkth(tre[p].right,k-lsz-1);
}

前缀 getpre

得到小于 k 的且最靠近 k 的数：

1. 按照 k-1 分裂成 x、y 两棵子树。
2. 使用 getkth() 求出 x 子树中最大的值，记为 ans。
3. 合并 x、y。
4. 返回 ans。

int getpre(int k){
    //按照k-1分裂出xy，则x中都是小于k的值
    //使用kth，求出x中最大值的值
    //最后合并
    int x,y,ans;
    split(root,x,y,k-1);
    ans=getkth(x,tre[x].sz);
    root=merge(x,y);
    return ans;
}

后缀 getsuf

和求前缀同理：

1. 按照 k 分裂成 x、y 两棵子树。
2. 使用 getkth() 求出 y 子树中最小的值，记为 ans。
3. 合并 x、y。
4. 返回 ans。

int getsuf(int k){
    //按照k分裂出xy，则y中的值都是大于k的值
    //使用kth，求出y中最小的值
    //最后合并
    int x,y,ans;
    split(root,x,y,k);
    ans=getkth(y,1);
    root=merge(x,y);
    return ans;
}

FHQ Treap 高端操作

接下来的操作几乎都是区间操作，比较牛逼高级。

区间操作的前提 split

由于正常的 FHQ Treap 以权值建立 BST，所以其区间是不连续的。所以我们想要对区间进行操作，就需要进行改动——以下标建立 BST。

以下标建立 BST 后，用类似前文的方法进行分裂，则分裂出的点处在一个连续区间中，所以可以方便的进行区间操作。

所以，我们可以根据下标写出新的 split() 函数。

代码中的 pushdown() 函数会在下文讲到。

void split(int p,int k,int &x,int &y){
    if(!p){x=y=0;return;}

    pushdown(p);//类似线段树的下传标记

    int left=tre[p].left,right=tre[p].right;
    if(tre[left].sz<k){
        x=p;
        split(right,k-tre[left].sz,right,y);
    }else{
        y=p;
        split(left,k,x,left);
    }
}

真的要改么? merge

由前文可知，merge() 函数完全依靠 rnd 值运行，不管 BST 维护的内容是什么，所以合并函数在理论上是不需要修改的。

但是，由于涉及到区间操作，我们引入了懒标记。所以需要加入 pushdown() 下传标记。

int merge(int x,int y){
    if(!x || !y) return x+y;

    if(tre[x].rnd<tre[y].rnd){
        pushdown(x);
        tre[x].right=merge(tre[x].right,y);
        pushup(x);
        return x;
    }else{
        pushdown(y);
        tre[y].left=merge(x,tre[y].left);
        pushup(y);
        return y;
    }
}

切割区间 cut

切割出来一个 l \sim r 的区间：

1. 按 l-1 分裂出子树 x、y。
2. 按照 r 把 y 分裂为 z、y。
3. z 即为所求。

int cut(int l,int r){
    int x,y,z;
    split(root,l-1,x,y);
    split(y,r,z,y);
    return z;
}

懒标记 pushdown

pushdown() 存在的意义和线段树一样，都是为了通过延迟更新的方式优化复杂度。

此处以区间推平为例，很明显，结构体的定义中要增加懒标记的相关变量。

struct Tre{
    int left,right;
    int val,rnd,sz;
    int lzy,lzy_num;
}tre[MN];

然后是更新节点内容，并下放懒标记。

void pushdown(int p){
    if(!tre[p].lzy) return;

    int left=tre[p].left,right=tre[p].right;

    tre[p].val=tre[p].lzy_num;

    tre[left].lzy=tre[right].lzy=tre[p].lzy;
    tre[left].lzy_num=tre[right].lzy_num=tre[p].lzy_num;

    tre[p].lzy=tre[p].lzy_num=0;
}