翘课写笔记。
1. 定义
竞赛图,即任意两点之前有且仅有一条边的有向图。即有向完全图,有 \dbinom{n}{2} 条边。
至于为什么叫竞赛图,就是赢得点向输的点连边,一个边代表的是胜负关系。
2. 性质
兰道定理(竞赛图判定)
我们定义比分序列为将每个点的出度 s_{i} 从小到大排序的序列。
那么若满足 \sum\limits_{i=1}^k s_{i}\ge \dbinom{k}{2} 且当 k=n 时取等(即 \sum\limits s=\dbinom{n}{2}),则一定能够造出一种竞赛图,反之不能。
必要性显然,考虑充分性证明,我们构造初始图,对于 j<i 则 i\to j 连边,设此时比分序列为 a,这个序列显然在上述条件能够取到等号。保持 \sum\limits_{i=1}^k a_{i}\le \sum\limits_{i=1}^k s_{i},不断调整图直到 a=s。
未构造完成时开头必然是一段等于后面接一个 a_{l}<s_{l},为了让后面的方法修改后使得 a 仍然有序,我们找到最后一个 a_{l}=a_{u} 的 u,显然有 a_{u}<s_{u}。因为总和固定,必然能找到第一个 v 使得 a_{v}>s_{v}。
此时有 a_{u}<s_{u}\le s_{v}<a_{v},有 a_{v}\ge a_{u}+2。
当 \exists v \to u,考虑翻转这条边,否则必然存在 p 使得 v \to p \to u,那么把路径反转。因为 a_{u}<s_{u},a_{i}\le s_{i},\forall i \in (u,v),不难证明反转后的序列仍然保持性质(\sum\limits a \le s)这样构造下去一定有解。
注意,这里定理都是存在,对于同一个比分序列可能对应本质不同的竞赛图。
兰道定理实质
兰道定理的实质是在一个序列和一定时,可以对于任意两个有关系(边)的位置进行相等量的调整(s_{i}\leftarrow s_{i}+v,s_{j}\leftarrow s_{j}-v),那么要判定任意一个值的序列是否与序列值的下界形式一样时,只需要判断是否每个前缀和都大于等于下界,以及最后的和与预期相等即可。证明考虑构造法不断调整。
竞赛图强连通分量个数(推论)
即:
其中 s 还是比分序列。证明如下:
G 缩点后形成了一条链,拓扑序上靠后的强连通分量里节点的出度一定严格小于靠前的强连通分量里节点的出度。考察链上相邻两个强连通分量 S, T,不妨假设 S 在拓扑序上比 T 靠前。我们一定能找到一个唯一的 x,使得 p_1 到 p_x 一一对应着 T 以及在拓扑序上比 T 更靠后的强连通分量里节点的出度。显然,\sum_{i=1}^x p_i = \binom{x}{2},因此 \sum_{i=1}^n \left[ \sum_{j=1}^i p_j = \binom{i}{2} \right] 不小于 G 的强连通分量个数。
同时,\forall x \in [1, n-1] \cap \mathbb{Z},\sum_{i=1}^x p_i = \binom{x}{2},p_{x+1} 到 p_n 对应的节点都向 p_1 到 p_x 对应的节点连边,所以 x 也唯一对应着链上相邻两个强连通分量的分界,因此 \sum_{i=1}^n \left[ \sum_{j=1}^i p_j = \binom{i}{2} \right] 不大于 G 的强连通分量个数。考虑如果说一个强连通分量被分成了两半,如果后一半和后继的度数和等于 \binom{n}{2} 的话说明后一半的出度达到了最小值,就不能向前一半有连边,所以前一半和后一半就缺少了构成强连通分量的桥梁,所以通过反证法不成立。
综上,\sum_{i=1}^n \left[ \sum_{j=1}^i p_j = \binom{i}{2} \right] 等于 G 的强连通分量个数。在求出出度序列后,通过桶排,我们可以 O(n) 求解一个 n 阶竞赛图的强连通分量个数。
缩点后呈链状
这是一个很重要的性质,所有与环,SCC相关的问题都可以用这个性质解决。
即竞赛图强连通缩点后的 DAG 呈链状, 拓扑序小的点向所有拓扑序比它大的点连边,如下图。
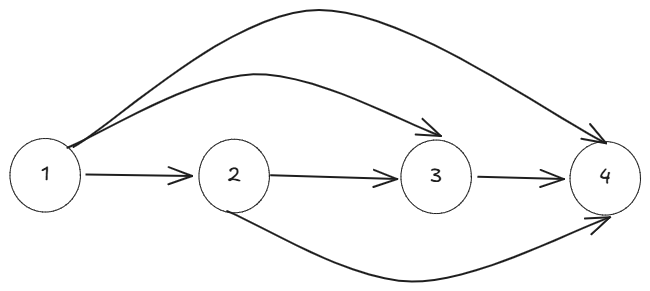
证明考虑归纳,考虑一个一个加入连通块。目前假设有一条链,设插入的为块为 x。若 x 连向所有点,放头,若所有点连向 x,放尾。否则找分界点插到中间即可(如果不能查到中间的话会成环)。
推论
- 若不存在位置 i 满足如下条件,则为强连通图:
- 在同一个SCC中在比分序列上是一个区间,根据比分序列可以完成拓扑排序。
利用拓扑序小的点向所有拓扑序比它大的点连边,从后向前扫,用一个和上面判断 SCC本质相同(只是左右端点不同)的式子判定即可。
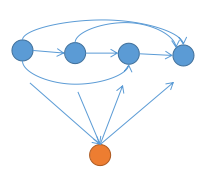
竞赛图存在一条哈密顿路径
证明,先缩点,如图构造:

竞赛图任意一个 SCC 存在一条哈密顿回路
考虑归纳, 逐点加入目前有一条链, 链上的每个强连通块都存在哈密顿回路,插入一个新点 x,只需证明新图中的强连通块都存在哈密顿回路即可。如果不产生新连通块, 就是呈链中讨论的情况, 否则一定存在一条 x 的出边在 x 入边左边, 随便找一对
如果是连到不同连通块, 见左图.
如果是同一连通块, 必定存在符合环的走向的相邻的一入一出, 见右图.
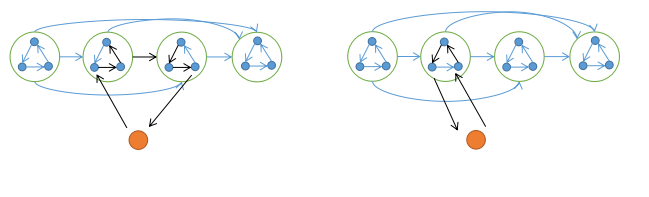
强连通竞赛图也算整体一个 SCC,也就是强连通竞赛图有哈密顿回路。
竞赛图若有环一定存在三元环
考虑找到任意一个环,讨论一下顺时针还是逆时针。
例如顺时针,考虑环中的边,若为逆,直接结束有三元环。若为顺向的边可以看做环少了因这条边存在而绕过的点。
始终不出现逆向的边,最后一条边处构成三元环。
竞赛图的k>=3个点的SCC中一定存在[3,k]元环
归纳法证明即可,作者懒了不证明了。
3. 例题
3.1 计数
不知名题
求 n 个点的强连通竞赛图个数。
考虑容斥,设 f(i) 表示 i 个点竞赛图个数,显然 f(i)=2^{\frac{i(i-1)}{2}},设 g(i) 表示 i 个点强连通竞赛图个数。
考虑转移,将图分成两部分,第一个部分是一个 SCC ,另外一个部分至少是一个 SCC ,枚举一个 j 个点的 SCC 进行转移。
CF850D Tournament Construction
m 及其小,而且值域很少,设一个图有 n 个点,则边数上界就是 30n,有 \dfrac{n(n-1)}{2}\le 30n,解得 n\le 61。
用兰顿定理可以判断是否合法,设 f(i,j,k) 表示能否用集合前 i 个元素,构造出 j 个点 k 条边的图,转移方程有:
让后考虑如何构造,发现可以发现一个竞赛图删除一个点以及它的所有边后仍然是一个竞赛图,那么避免冲突每次选择最小出度的点 更新边以及其他点的出度即可。
#include<bits/stdc++.h>
using namespace std;
constexpr int MN=80,MM=2520;
int m,n=1,a[MN],ret[MM],tmp[MM],ans[MN][MN];
bool f[MN][MN][MM];
bool cmp(int x,int y){
return ret[x]<ret[y];
}
void dfs(int x,int y,int z){
if(!x) return;
ret[x]=a[y];
z-=a[y];
x--;
if(f[x][y][z]) dfs(x,y,z);
else dfs(x,y-1,z);
}
void getans(){
for(int i=1;i<=n;i++) tmp[i]=i;
for(int i=1;i<=n;i++){
sort(tmp+i,tmp+n+1,cmp);
for(int j=i+1;j<=i+ret[tmp[i]];j++){
ans[tmp[i]][tmp[j]]=1;
}
for(int j=i+ret[tmp[i]]+1;j<=n;j++){
ans[tmp[j]][tmp[i]]=1;
ret[tmp[j]]--;
}
}
}
int main(){
cin>>m;
for(int i=1;i<=m;i++){
cin>>a[i];
}
sort(a+1,a+1+m);
f[1][1][a[1]]=1;
while(n<62&&(n<m||!f[n][m][n*(n-1)/2])){
n++;
for(int i=1;i<=m;i++){
for(int j=(n-1)*(n-2)/2;j<=(n-1)*a[m];j++){
if(f[n-1][i][j]){
f[n][i][j+a[i]]=1;
if(i+1<=m) f[n][i+1][j+a[i+1]]=1;
}
}
}
}
if(n>61){
cout<<"=(";
return 0;
}
dfs(n,m,n*(n-1)/2);
getans();
cout<<n<<'\n';
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<ans[i][j];
}
cout<<'\n';
}
return 0;
}
BZOJ 5219 最长路径 竞赛图组合计数
计数从 1 出发的最长简单路径经过点数恰好为 i 的竞赛图个数。i\in [1,n],1\le n \le 2000
竞赛图有个很好的性质:一定存在一条哈密尔顿路径。
考虑设 f(i,j) 表示 i 个点,最长路径为 j 的竞赛图数量。
显然有 f(i,i) 为强连通竞赛图,但是这里我们可以不用像上面不知名题求,就用容斥 f(i,i)=2^{\frac{i(i-1)}{2}}-\sum\limits_{j=1}^{i-1} f(i,j) 即可。
考虑 f(i,1) 可以构造出所有 1 号点的边连向 1 号点即可,有 f(i,1)=2^{\frac{(i-1)(i-2)}{2}}。
那么剩下的怎么求,考虑将图划分为两个块,一个块是供 1 走的块,剩下的块不给 1 走,但是可能不存在不给 1 走的块。
那么有 f(i,j)=f(j,j) \times \binom{i-1}{j-1} \times 2^{\frac{(i-j)(i-j-1)}{2}},考虑 j 个点连通块的连边方式,让后要选点,在把剩下的连边即可。
时间复杂度 O(n^2),但是可怕的是 BZOJ 挂了,有谁好心传个原题?
CF913F
令 p=\dfrac{a}{b}。
考虑倒推答案,设 f(i) 表示 i 个点的期望答案,g(i) 表示形成大小为 i 的 SCC 概率,h(i,j) 表示 i 个人打比赛,其中 j 个人被 (i-j) 个人打赢的概率。
最后一个 SCC 的大小,有:
但是 f(i) 会转移到自己,要解方程,这里不过多叙述。
考虑 g_{i} 如何求,考虑只要图中没有点被其它点都吊打的情况它就是强联通图,那么转移:
考虑 h,对于新加入一个点,如果在 j 中那么输给 i-j,反之要赢 j 个点,那么有:
时间 O(n^2)。
3.2 SCC 及其拓展
CF1268D
两个结论:
- 对于 n\ge 4,n 阶强联通竞赛图具有 n-1 阶强联通子图。
- 对于 n\ge 7,n 阶竞赛图存在一种翻转方案使得只需要翻转一个结点就能让它强联通。
对于 n\le 6,暴力枚举翻转结点即可,对于 n>6 考虑枚举每个位置翻转并检查就好了。我们可以用兰顿定理的推论(上面有讲)来快速判断是否强连通。
证明可以看其他题解:题解 CF1268D 【Invertation in Tournament】
#include<bits/stdc++.h>
using namespace std;
constexpr int MN=2520,MOD=998244353;
int n,cf[MN],h[MN];
bool mp[MN][MN];
bool check(){
sort(cf+1,cf+1+n);
for(int i=2;i<=n;i++) cf[i]+=cf[i-1];
for(int i=1;i<n;i++){
if(cf[i]==i*(i-1)/2) return 0;
}
return 1;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
char c;
cin>>c;
mp[i][j]=c-'0';
h[i]+=mp[i][j];
}
}
for(int i=1;i<=n;i++) cf[i]=h[i];
if(check()){
cout<<"0 1";
return 0;
}
int ret=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) cf[j]=h[j];
for(int j=1;j<=n;j++){
cf[i]-=mp[i][j]*2-1;
cf[j]+=mp[i][j]*2-1;
}
if(check()) ret++;
}
if(ret){
cout<<1<<" "<<ret;
return 0;
}
if(n==4) cout<<-1;
if(n==6) cout<<"2 18";
return 0;
}
P3561 [POI 2017] Turysta
定理上面都讲完了,先缩点,然后对于每个强连通分量,求哈密顿回路。然后就可以对任意一个强连通分量任意点进,任意点出了。
怎么构造可以去看其他题解的构造。
#include<bits/stdc++.h>
using namespace std;
constexpr int MN=2e3+15;
int n,tcnt,nxt[MN],a[MN][MN],in[MN],tpos[MN],pos[MN];
vector<int> adj[MN],G[MN],dcc[MN],ans[MN];
namespace Tarjan{
int dfn[MN],low[MN],s[MN],col[MN],ctot,top,dtot;
bool vis[MN];
void tarjan(int u){
low[u]=dfn[u]=++dtot;
s[++top]=u;
vis[u]=1;
for(auto v:adj[u]){
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(vis[v]){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
ctot++;
int p;
do{
p=s[top--];
col[p]=ctot;
vis[p]=0;
}while(p!=u);
}
}
}using namespace Tarjan;
void toposort(){
queue<int> q;
for(int i=1;i<=ctot;i++){
if(!in[i]) q.push(i);
}
while(!q.empty()){
int u=q.front();
q.pop();
tpos[++tcnt]=u;
pos[u]=tcnt;
for(auto v:G[u]){
in[v]--;
if(!in[v]) q.push(v);
}
}
}
void getham(int c){
if(dcc[c].size()==1) return;
int s=dcc[c][0],t=s;
for(int i=1;i<dcc[c].size();i++){
int x=dcc[c][i];
if(a[t][x]) nxt[t]=x,t=x;
else if(a[x][s]) nxt[x]=s,s=x;
else{
for(int j=s;j!=t;j=nxt[j]){
if(a[j][x]&&a[x][nxt[j]]){
nxt[x]=nxt[j];
nxt[j]=x;
break;
}
}
}
}
t=0;
for(int i=nxt[s];i;i=nxt[i]){
if(t){
if(a[i][s]){
t=i;
continue;
}
for(int j=s,k=nxt[s];j!=t;j=k,k=nxt[k]){
if(a[i][k]){
nxt[j]=nxt[t];
nxt[t]=s;
s=k;
t=i;
break;
}
}
}else if(a[i][s]) t=i;
}
nxt[t]=s;
}
int main(){
cin>>n;
for(int i=2;i<=n;i++){
for(int j=1;j<=i-1;j++){
int x;
cin>>x;
if(x){
adj[j].push_back(i);
a[j][i]=1;
}else{
adj[i].push_back(j);
a[i][j]=1;
}
}
}
for(int i=1;i<=n;i++){
if(!dfn[i]) Tarjan::tarjan(i);
}
for(int i=1;i<=n;i++){
dcc[col[i]].push_back(i);
}
for(int u=1;u<=n;u++){
for(auto v:adj[u]){
if(col[u]!=col[v]){
G[col[u]].push_back(col[v]);
in[col[v]]++;
}
}
}
toposort();
for(int i=1;i<=tcnt;i++){
getham(tpos[i]);
}
for(int i=1;i<=n;i++){
int lst=i,now=pos[col[i]];
while('QWQ'){
if(dcc[tpos[now]].size()==1){
ans[i].push_back(lst);
if(now==tcnt) break;
lst=dcc[tpos[++now]][0];
continue;
}
ans[i].push_back(lst);
for(int j=nxt[lst];j!=lst;j=nxt[j]){
ans[i].push_back(j);
}
if(now==tcnt) break;
lst=dcc[tpos[++now]][0];
}
}
for(int i=1;i<=n;i++){
cout<<ans[i].size()<<' ';
for(auto p:ans[i]) cout<<p<<" ";
cout<<'\n';
}
return 0;
}
.png)