前言
树剖的基本思想是将树按一定方式剖分成若干条重链,重链便转化为了序列,随后我们就可以使用线段树来维护这序列上的值,这样,树上的修改与查询就成为了序列上的修改与查询,以达到更优时间复杂度的目的。
本篇题解将着重讲解树剖相关内容,对此,你需要学习的前置知识有:
树剖基本内容
对于树剖这种方法具体如何剖分一颗树。我们由浅入深,逐步来讲解。
相关定义
- 重儿子:某个父节点的儿子中,子树大小(也就是子树中节点最多的)最大的节点。(同时规定一个节点的重儿子只有一个)
- 轻儿子:某个父节点的儿子中,非重儿子的节点。
- 重边:父节点与其重儿子连成的边。
- 轻边:父节点与其轻儿子连成的边。
- 重链:由多条重边连成的链。(叶子节点单独成链)
放一张图辅助理解:
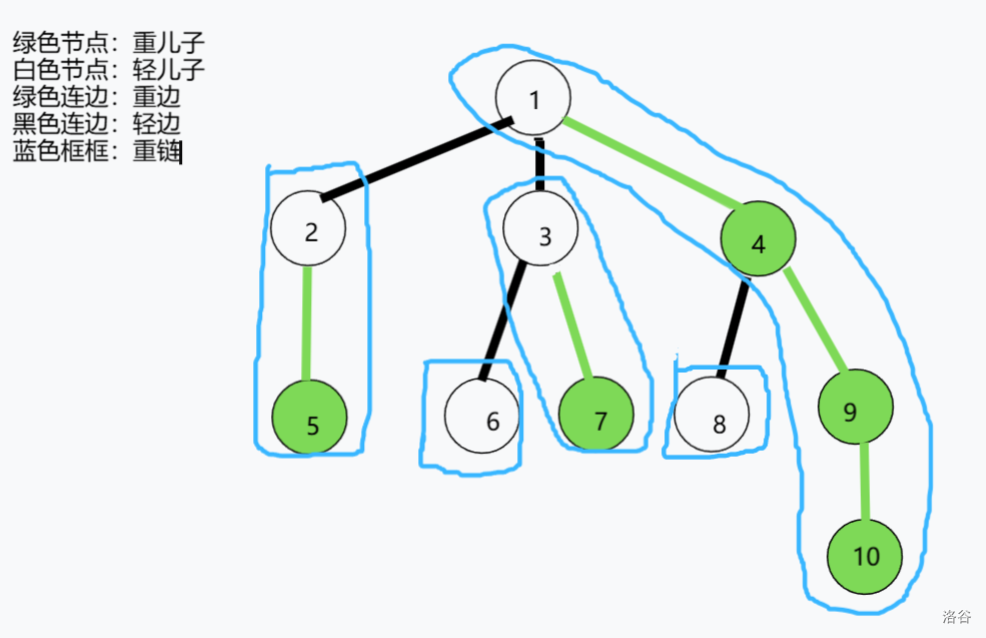
上图内容不难从定义推得,我挑取一部分详细解释一下(认为自己能够完全理解定义的同学可以跳过了):
- 1 节点的重儿子是 4(其子树大小为 4 并且无法在 1 节点的其他儿子节点找到子树大小更大的)。
- 2 节点的重儿子是 5(因为只有一个儿子,所以你当然无法找到第二个子树大小更大的)。
- 3 节点的重儿子可以在 6 或者 7 中任意选得,因为它们的子树大小是一样的,但我们需要保证一个子树的重儿子只有一个。
- 1 节点到 10 节点连成的重链中 4 是 1 的重儿子,9 是 4 的重儿子,10 是 9 的重儿子。
- 节点 6 没有重儿子,单独成链(因为我们要让树全部剖分成链,如果没有重边连成重链,就单独成链),同理,节点 8 也是。
性质
我们再次观察上图,不难发现有如下性质:
- 当前节点 x 每次向下走一条轻边到达轻儿子 y,自身的子树大小至少除以 2。(否则 y 就应该变为 x 的重儿子)
- 每条重链的链顶一定是轻儿子。
- 任意两点的路径可以被不超过 \log{n} 条链覆盖。(可以从性质第一条推导)
详细实现
上述定义已经足够我们把一棵树剖分成若干条链了,接下来我们结合代码详细说明一下其实现流程。
我们通常使用两次 dfs 来实现树剖,同时,你还需要记录如下变量:
- siz[i] 子树大小。
- dep[i] 深度。
- fa[i] 记录父节点。
- hson[i] 记录重儿子。
- top[i] 记录当前节点所在重链的链顶。
- id[i] 记录当前节点被拍成序列后,在序列上的新编号。
- id\_val[i] 表示新序列上第 i 个数的值。
第一遍 dfs
维护了前四个变量。
遍历了整棵树求解节点信息,时间复杂度 O(n)。
// 当前节点 父节点
void dfs1(int x,int f){
siz[x]=1;//siz数组先初始化为1,表示目前自身大小为1
fa[x]=f;//记录父节点
dep[x]=dep[f]+1;//深度比父节点深1
for(int i=head[x];i;i=e[i].next){//遍历子节点
int y=e[i].to;
if(y!=f){//注意别遍历回去了
dfs1(y,x);
siz[x]+=siz[y];//递归回来时,子节点的大小已经被计算完毕,直接加给父节点
//每次递归判断是否能够更新重儿子节点
if(siz[hson[x]]<siz[y] || !hson[x]){
hson[x]=y;
}
}
}
}
第二遍 dfs
用于求解后三个变量。
注意我们求解 top[i] 时,有重儿子要先遍历重儿子,直到找不到重儿子再返回。
这是因为沿着重边一路走下去的节点一定在同一条重链,其链顶是一样的,如果找不到重儿子,则说明该重链结束了,需要重新传入链顶参数进行新重链的求解。
同样,在求解 id[i] 和 id\_val[i] 时也要遵循重儿子先行的顺序,至于为什么这样做对时间复杂度来说是优的,在下面具体讲题意操作时会谈到。
遍历了一遍整棵树,时间复杂度 O(n)。
// 当前节点 链顶
void dfs2(int x,int t){
top[x]=t;//记录当前节点所在链的链顶
id[x]=++cnt;//记录当前节点在序列中的新编号
id_val[cnt]=a[x];//当前节点的值直接赋给它对应的编号就好了
if(!hson[x]) return ;//如果找不到重儿子就返回
else dfs2(hson[x],t);//继续求解当前重链
//递归后说明重链已经走完,接下来遍历轻儿子
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
//这里的判断很容易理解,不能走到父节点还需要满足是轻儿子
if(y!=fa[x] && y!=hson[x]){
dfs2(y,y);//根据性质,轻儿子就是当前新重链的链顶
}
}
}
小结
现在我们就成功的把一棵树剖分成了若干条链,同时也把树上的点按重儿子先行的规则拍成了序列,放一张图,我们具体观察一下我的树现在具有什么样的性质。
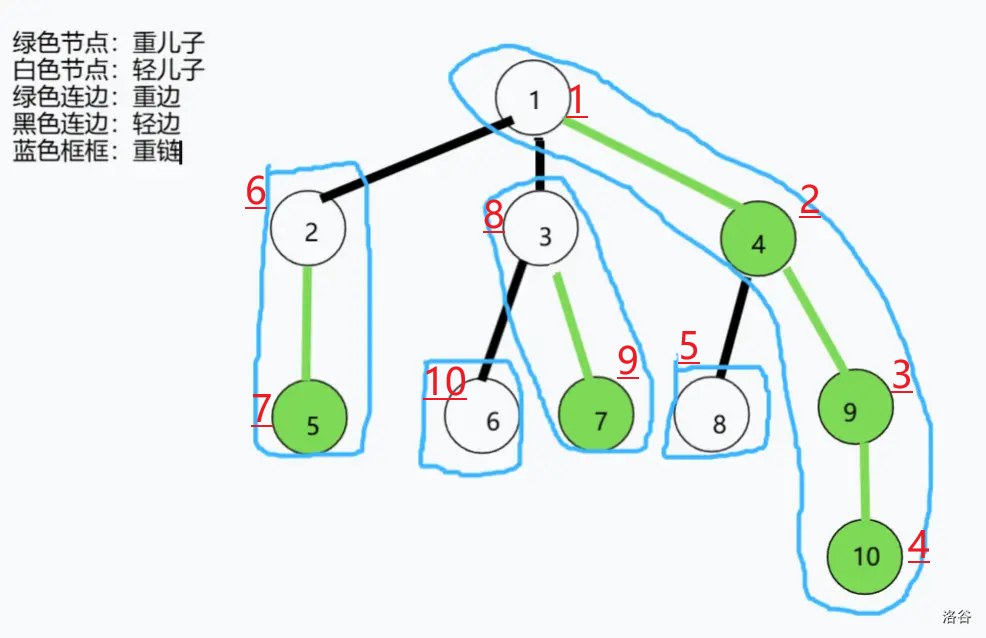
现在红色字体是我们根据程序模拟出来的个节点在序列上的新编号,不难发现:同一条重链上的节点,在序列上的编号是连续的,结合之前所讲的性质 3,你也许隐隐约约对树剖为什么能更快地求解树上的修改与查询有了答案。
如果没有想到也没关系,我们马上根据题意讲解题意操作并给出复杂度证明!
题意操作
由于题意上的操作都是形如 x 到 y 的最短路径上的查询与修改,或者以 x 为根的子树里的查询与修改。同时考虑到我们刚才把树剖成了序列,所以对于序列的区间修改与查询,我们使用线段树进行快速维护。
为使文章精简,线段树部分的代码不再展示与讲解,有需求的同学在可以先自学或者在本文最下方完整代码处查看。
同时也为了文章必要的清晰与读者的观感,我们约定:
change()为线段树的区间加操作。query()为线段树的区间查询操作。
操作一:树从 x 到 y 结点最短路径上所有节点的值都加上 z
在一棵树上 x 到 y 的最短路径为,从 x 到 x 和 y 的 LCA(最近共祖先),再到 y。又因为两点间的最短路径被若干条重链覆盖着。我们便容易想到,从链顶更深的点开始,每次操作一条链,再不断交替着往上跳出已经修改的链,直到修改到两点已经在同一条链中。
放一张图,大家可以了解一下是怎么不断跳链的。
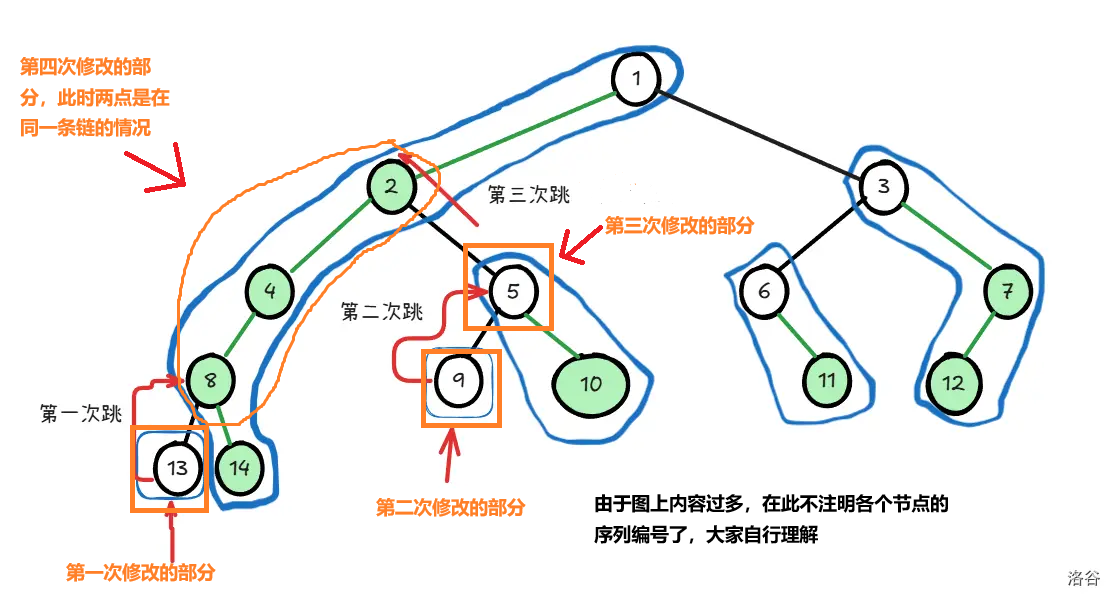
代码实现:
void changeto(int x,int y,int z){//x到y都加上z
while(top[x]!=top[y]){//两个点不在同一条链上
if(dep[top[x]]<dep[top[y]]){//每次要让链顶深度更深的跳,否则两点越来越远
swap(x,y);
}
//修改这条链的链顶到该点在序列上的区间
change(1,id[top[x]],id[x],z);
//跳出这条链
x=fa[top[x]];
}
//当它们在同一条链上时
//只剩两点间的区间未修改
if(id[x]>id[y]){//保证左区间小于右区间
swap(x,y);
}
change(1,id[x],id[y],z);
}
单次操作一时间复杂度
根据上面讲过的性质 3,任意两点的路径可以被不超过 \log{n} 条链覆盖。意思是我们一次操作一不会在超过 \log{n} 条链上调用线段树的 change() 函数,又由线段树一次区间修改的时间复杂度为 O(\log{n}) 级别。
故单次操作一的总时间复杂度为 O(\log^2{n}) 。
现在你应该知道我们为什么使用树剖在链上操作会快了,我们继续看接下来的操作。
操作二:求树上从 x 到 y 结点最短路径上所有节点的值之和
类比我们的操作一,操作二也很好想了,两点不断跳出链,每次跳前查询一下该点到链顶的区间和,最后加到一起输出。
直接给出代码:
long long queryto(int x,int y){
long long ans=0;
while(top[x]!=top[y]){//不在同一条链
if(dep[top[x]]<dep[top[y]]){//链顶深的先跳
swap(x,y);
}
//统计链顶到该点的区间和
ans=(ans+query(1,id[top[x]],id[x]));
//跳出链
x=fa[top[x]];
}
if(id[x]>id[y]){
swap(x,y);
}
//统计最后一段区间
ans=ans+query(1,id[x],id[y]);
//返回答案即可
return ans;
}
单次操作二时间复杂度
同样的原因,一共不会超过 \log{n} 条链,并且线段树单次查询的时间复杂度为 O(\log{n}) 级别。
故单次操作二的时间复杂度为 O(\log^2{n})。
操作三:将以 x 为根节点的子树内所有节点值都加上 z
重新来看这张图。

先给出结论:对一个节点进行 dfs 时,该节点及其子树会形成一段连续的区间,区间的末尾是最后一个被 dfs 的节点。
这一点不难理解,如果当前节点的子树还未被 dfs 完毕,此时是不会回溯出来到别的位置进行 dfs 的。
故这个操作只需我们调用一下 change() 函数即可:
change(1,id[x],id[x]+siz[x]-1,z);
//从x的编号开始,修改到id[x]+siz[x]-1
//即最后一个被dfs的节点。
单次时间复杂度 O(\log{n}) ,不细讲。
操作四:查询以 x 为根节点的子树内所有节点值之和
与操作三同理,直接查询 x 到其子树里最后一个被 dfs 的节点的区间即可。
query(1,id[x],id[x]+siz[x]-1)
单次时间复杂度 O(\log{n}),不细讲。
小结
至此,所有操作已经讲解完毕。您又学会了一种新算法,拜谢%%%。
总时间复杂度
单次操作最高的时间复杂度在 O(\log^2{n}) 级别,共有 m 次操作。
故总时间复杂度 O(m\log^2{n})。
完整代码
题目还要求对p取模,但我为了美观,就没在讲解时加,大家写的时候记得加上,同时注意可能存在负数,对负数取模时要先加模数再取模。
#include<bits/stdc++.h>
#define ls i<<1
#define rs i<<1|1
using namespace std;
const int N=1e5+5;
struct {
int next,to;
}e[N<<1];
int tot,head[N];
int dep[N],siz[N],hson[N],fa[N];
int top[N],id[N],cnt;
int n,m,r,p,a[N],id_val[N];
struct node{
int l,r;
long long sum;
long long add;
}t[N<<2];
void add(int x,int y){
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
}
//-----------------------------
//线段树
void pushup(int i){
t[i].sum=(t[ls].sum+t[rs].sum+p)%p;
}
void build(int i,int l,int r){
t[i].l=l;
t[i].r=r;
if(l==r){
t[i].sum=id_val[l]%p;
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(i);
}
void spread(int i){
if(t[i].add){
t[ls].sum=(t[ls].sum+t[i].add*(t[ls].r-t[ls].l+1)+p)%p;
t[rs].sum=(t[rs].sum+t[i].add*(t[rs].r-t[rs].l+1)+p)%p;
t[ls].add+=t[i].add;
t[rs].add+=t[i].add;
t[ls].add%=p;
t[rs].add%=p;
t[i].add=0;
}
}
void change(int i,int l,int r,int v){
if(l<=t[i].l && r>=t[i].r){
t[i].sum=(t[i].sum+v*(t[i].r-t[i].l+1)%p+p)%p;
t[i].add+=v;
t[i].add%=p;
return;
}
spread(i);
int mid=(t[i].l+t[i].r)>>1;
if(l<=mid){
change(ls,l,r,v);
}
if(r>mid){
change(rs,l,r,v);
}
pushup(i);
}
long long query(int i,int l,int r){
if(t[i].l>r||t[i].r<l){
return 0;
}
if(l<=t[i].l&&t[i].r<=r){
return t[i].sum;
}
spread(i);
return (query(ls,l,r)+query(rs,l,r)+p)%p;
}
//----------------------
//树剖
void dfs1(int x,int f){
siz[x]=1;
fa[x]=f;
dep[x]=dep[f]+1;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y!=f){
dfs1(y,x);
siz[x]+=siz[y];
if(siz[hson[x]]<siz[y] || !hson[x]){
hson[x]=y;
}
}
}
}
void dfs2(int x,int t){
top[x]=t;
id[x]=++cnt;
id_val[cnt]=a[x];
if(!hson[x])return ;
dfs2(hson[x],t);
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y!=fa[x] && y!=hson[x]){
dfs2(y,y);
}
}
}
void changeto(int x,int y,int z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]){
swap(x,y);
}
change(1,id[top[x]],id[x],z);
x=fa[top[x]];
}
if(id[x]>id[y]){
swap(x,y);
}
change(1,id[x],id[y],z);
}
long long queryto(int x,int y){
long long ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]){
swap(x,y);
}
ans=(ans+query(1,id[top[x]],id[x])+p)%p;
x=fa[top[x]];
}
if(id[x]>id[y]){
swap(x,y);
}
ans=(ans+query(1,id[x],id[y])+p)%p;
return ans;
}
//---------
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin>>n>>m>>r>>p;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n-1;i++){
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
dfs1(r,0);
dfs2(r,r);
build(1,1,n);
for(int i=1;i<=m;i++){
int opt,x,y,z;
cin>>opt;
if(opt==1){
cin>>x>>y>>z;
changeto(x,y,z);
}
if(opt==2){
cin>>x>>y;
cout<<queryto(x,y)<<'\n';
}
if(opt==3){
cin>>x>>z;
change(1,id[x],id[x]+siz[x]-1,z);
}
if(opt==4){
cin>>x;
cout<<query(1,id[x],id[x]+siz[x]-1)<<'\n';
}
}
return 0;
}
后记
在上述讲解时提到了最近公共祖先,同学们不难发现使用树剖求解最近公共祖先也是一种可行的方式,并且常数小,实际运行速度非常可观,应该可以说比同时间复杂度的算法都优秀(但不绝对)感兴趣的同学可以看我的另一篇题解:题解:P3379 【模板】最近公共祖先(LCA)。(你就会发现我用的图都是旧的)
至此所有内容已经讲解完毕,笔者力求语言简洁直观,希望大家看到这篇题解都能有所收获,若有不足之处,欢迎私信批评指出,笔者一定认真倾听。
完结撒花!!!
.png)