题面
描述
有一棵n个节点的有根树,从根开始执行深度优先遍历,每次选择未遍历过的节点编号P_{i}最小的子节点继续向下遍历,给出先序遍历(DFS序),求共有多少不同的树满足这个先序遍历?
两棵有根树(根节点为1)被视为不同,当且仅当两棵树中存在编号相同但父节点不同的节点
约束
- 2 \leq n \leq 500
- 1 \leq P_{i} \leq n,\,P_{1}=1,\,任意两个P_{i}互不相同
题解
思路
这道题码量不大,但是一道思维好题。
这题我按照学长的思路打了一遍,但只能过几个点,也许是我太蒟蒻,没有判断好条件,后来看题解很多都写得不太清楚,于是我打算梳理一下我的思路,亦希望能把这道题给说清楚。ok,talk\ is\ cheap,\,show\ me\ the\ code!
首先,我们要根据题中的条件找到一些性质
- 先序遍历:根、依次子节点
先序遍历给到我们,我们最容易确定的是根,那么如何确定其子节点?一个树上的问题,却给我们一个序列,是不是可以将树上的问题转化为序列问题求解?
思考这道题所给的先序遍历和树的结构有何关联?
首先,第一个元素是根节点,第二个元素是它的第一个子节点……
我们先序遍历一定是一个一个子节点进行遍历,并且根据题中所给的约束,子节点遍历的顺序是根据子节点编号从小到大,所以我们是不是可以枚举一个合适的节点,将当前遍历的区间划分为两个部分。从而将大问题化为没有后效性的子问题,所以我们可以用区间DP来解决这道题。
既然是区间DP,那么dp状态中要体现区间的性质,设f[i][j]表示以i为根节点,i+1\sim j为其子树下节点能够组成的不同树的个数。
那么我们就可以枚举k来当作断点,f[i+1][k]为一部分,f[k+1][r]为另一部分,这两部分是相互独立的,根据乘法原理,f[i][j]加上f[i+1][k]\times f[k+1][r]的贡献即可。
但是事情还远没有这么简单,我们考虑细节问题
首先,我们理解一下这个状态转移方程,我们可以把i+1,k看作一个以i+1为根的子树,将[k+1,j]看作其他的子树(注意:这里不一定是二叉树),那么这里就会出现问题f[k+1][j]表示以k+1为根,以[k+2,j]的节点为其子树节点的树的情况数,也就是说我们把不知道是几个儿子的树强行变成了二叉树,那么就无法统计到正确的情况数,我们可以用一点小技巧来解决这个问题,如下图
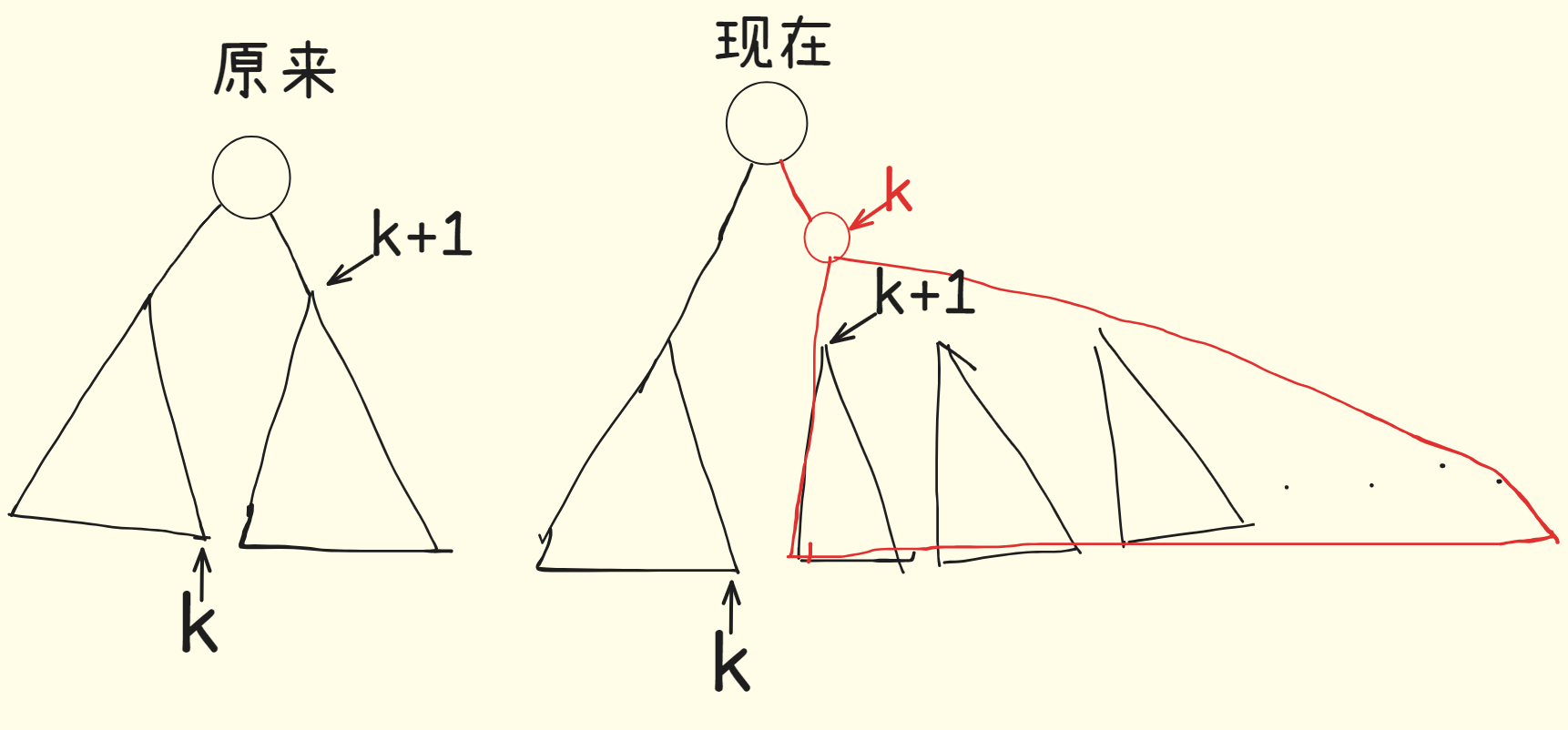
我们可以用一个所谓的"虚拟节点",也就是图中红色的k来作为左边部分的根节点,这样就能包含多叉树的情况了。
下面我们来处理题中的约束,即 每次选择未遍历过编号最小的子节点 我们真实的下一个根节点是k+1,所以我们要确保P_{k+1}>P_{i+1},当然,这里有一种特殊情况,就是右边没有子树,也就是k==j,这种情况也可以用下面的方程转移
最后的正确转移方程
code
const int N = 510, mod = 998244353;
typedef long long ll;
int n, a[N];
int f[N][N];
int main () {
memset(f, 0, sizeof f);
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
f[i][i] = 1;
}
for (int len = 2; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
for (int k = i + 1; k <= j; k++) {
if (a[k + 1] > a[i + 1] || k == j) {
f[i][j] = (f[i][j] + (ll)f[i + 1][k] * f[k][j]) % mod;
}
}
}
}
printf("%d\n", (f[1][n] + mod) % mod);
return 0;
}
.png)