注：线性代数并不算于这篇文章

0.前言

数论应该算是oi里面一个比较算是重要的章节了吧，他在大纲内标得难度居然比平衡树还简单？听老师说这个难度其实是按学起来的难度表的。应用起来和平衡树的区间操作一样难。

故借一个下午，整理数论笔记，重新思考思考一下吧。

数论研究的是整数的性质，但是性质要好多啊啊啊。一个一个慢慢学吧.

1.扬帆启航——整除

整除应该早就在小学中学过他的概念了。这里我们添加几个符号来表示整除，并且重新复述一遍定义。

若a和b为整数，a整除b。则b是a的倍数，a是b的约数（或者也可以叫做因数），我们记为a|b。整除的大部分性质都是显而易见的，如下

1.任意性

若a|b，则对于任意非零整数m，有am|bm。

2.传递性

若a|b且b|c，则a|c。

3.可消性

若a|bc且a与c互素，则a|b

4.组合性

若c|a且c|b，对于任意整数m,n，有c|(ma+nb)

2.数论的基础——素数

1.素数的定义

素数又称质数，其满足性质就是大于等于2，并且除了1和他本身外不能被其他的任何自然数整除。
不满足该性质的数为合数，但是1既不是素数又不是合数
2是唯一的偶素数
随着整数的增大，素数的分布越来越稀疏。随机整数x是素数的概率是\frac{1}{log_2x}，

2.素数判定

怎样取判定一个数是否为素数？我们先从定义来看，素数表示只能被1和自己整除的正整数。那我们就可以得到如下的做法

朴素判定：对n做[2,n)范围的余数判定，如果至少一个数取余n后为0，则n为合数，反之为素数，时间复杂度O(n)。

我们考虑一下优化，假设一个数能够整除n，即a|n，那么\frac{n}{a}也一定能够整除a，那么不妨设a\le \frac{n}{a} ，可得a^2\le n，可得a\le \sqrt{n} ，也就是说我们只需要筛到\sqrt{n}就可以了，时间复杂度就降到了\sqrt{n}，

优化判定:对n做[2,\sqrt{n}]的判定，同朴素筛法取余，时间复杂度O(\sqrt{n})

要不要再快点？我们显然可得如果n是合数，那么必然有一个小于等于\sqrt{n}的素银子，只需要对\sqrt{n}范围内的素数进行测试即可，假设该范围内的素数个数为s，则时间复杂度为O(s)

不过，我们发现这个的复杂度只能在10^{12}内管用，往外就超时了，我们可以使用Miller_Rabin算法来求解，下文在费马小定理会提到。

3.素数筛法

给定n，求[2,n]内所有素数

像上面一样逐个判断会很慢，我们可以用“筛子”，来一起筛所有的整数，把合数都筛掉。常用的两种算法分别为埃式筛和欧拉筛。

1.埃式筛

我们直接利用素数的定义，即除了1和他本身外不能被其他的任何自然数整除。可以得出他的倍数都是合数。

步骤如下

用一个标记数组f[maxn]，其中f[i]=0表示i为素数否则为非素数。首先先把f[0]=f[1]=1，因为他们都不是素数
从未被标记的数中找到最小的数，为2，它不是任何（除1与其本身）数的倍数，所以2是素数，这时候我们将4，6，8，10，...等2的倍数标记为1
从未被标记的数中找到最小的数，为3.它也是素数，我们把它的倍数也标记上，6，9，12....
从未被标记的数中找到最小的数，为5，它也是素数，我们标记他的倍数，10，15，20，25.....
..........

这种方式我们遍历完标记数组f[i]，如果没有标记1，就是素数。这种的时间复杂度就是O(nloglogn)，已经十分接近线性了。

如果我们对于f数组使用vector<bool>或者bitset进行优化可以将效率大幅提高。

vector<int> prime;

vector<bool> notprime(100000000);

void aishi(int n){

    for(int i=2;i<=n;i++){

        if(notprime[i]!=1){

            prime.push_back(i);

            for(int j=i*2;j<=n;j+=i){

                notprime[j]=1;

            }

        }

    }

}

但是带log，当数量级增大的时候就会TLE。我们考虑上面的情况（重复划掉），我们发现有重复的数组被筛掉，我们能否优化掉这一过程呢

2.欧拉筛（线性筛）

原理就是一个合数肯定有一个最小质因数。让每个合数被他的最小质因数筛选一次，以达到不重复筛的目的，步骤如下

逐一检查[2,n)的所有数，第一个数2是素数，取出来
当检查到第i个数的时候，利用已经求过的素数取筛到对应的合数x，而且用x的最小质因数取筛

代码如下

vector<bool> notprime(MN+5);

vector<int> prime;

void shai(){

    for(int i=2;i<=n;i++){

        if(!notprime[i]){

            prime.push_back(i);

        }

        for(int j=0;j<prime.size();j++){

            if(i*prime[j]>n) break;

            notprime[i*prime[j]]=1;

            if(i%prime[j]==0){

                break;

            }

        }

    }

}

我们可以比较一下埃式筛和线性筛的性能差距，都使用了vector优化

线性筛

埃式筛

飞快

3.算数唯一分解定理

我们来看素数真正的定义，也就是算数基本引理

设p是素数，若p|a_1 a_2那么p|a_1和p|a_2至少有一个成立

算数唯一分解定理表示如下

设正整数a，都可以唯一分解成素数的乘积，如下
n=p_1p_2p_3...p_k（p_1\le p_2\le p_3\le...\le p_k），这里素数并不要求是一样的，我们可以将相同的素数合并变成幂的形式，如下
n=p^{e_1}_{1}p^{e_2}_{2}...p^{e_k}_{k} 。

遇到一个数不要只把它当作一个普普通通的数，要想到算数唯一分解定理。

4.素因子分解

还是靠经典的试除法，考虑朴素算法，因数是成对分布的，的所有因数可以被分成两块，即[2,\sqrt{n}]和 [\sqrt{n}+1,n]。只需要把[2,\sqrt{n}]里的数遍历一遍，再根据除法就可以找出至少两个因数了。这个方法的时间复杂度为 O(\sqrt{n})。

代码如下(粘贴自oiwiki)

vector<int> breakdown(int N) {

  vector<int> result;

  for (int i = 2; i * i <= N; i++) {

    if (N % i == 0) {  // 如果 i 能够整除 N，说明 i 为 N 的一个质因子。

      while (N % i == 0) N /= i;

      result.push_back(i);

    }

  }

  if (N != 1) {  // 说明再经过操作之后 N 留下了一个素数

    result.push_back(N);

  }

  return result;

}

证明result中所有元素是N的全体素因数

首先考察 N 的变化。当循环进行到 i 结束时，由于刚执行结束 while(N % i == 0) N /= i 部分，i 不再整除 N。而且，每次除去一个因子，都能够保证 N 仍整除。这两点保证了，当循环进行到 i 开始时，N 是的一个因子，且不被任何小于 i 的整数整除。
其次证明 result 中的元素均为的因子。当循环进行到 i 时，能够在 result 中存入 i 的条件是 N % i == 0，这说明 i 整除 N，且已经说明 N 是的因子，故而有 i 是的因子。当对 i 的循环结束时，若 N 不为一，也会存入 result。此时它根据前文，也必然是的一个因子。
其次证明 result 中均为素数。我们假设存在一个在 result 中的合数，则必然存在 i 不超过 $\sqrt K$ ，满足 i 是 K 的一个因子。这样的不可能作为循环中的某个 i 存入 result，因为第一段已经说明，当循环到时，N 不被任何小于的 i 整除。这样的也不可能在循环结束后加入，因为循环退出的条件是 i * i > N，故而已经遍历完了所有不超过 $\sqrt K$ 的 i，而且据上文所说，这些 i 绝不能整除目前的 N，亦即。
最后证明，所有的素因子必然出现在 result 中。不妨假设是的一个素因子，但并没有出现在 result 中。根据上文的讨论，不可能是循环中出现过的 i。设 i 是退出循环前最后的 i，则 i 严格小于，而退出循环后的 N 不被之前的 i 整除，故而整除 N。所以最后的 N 大于一，则根据前文所述，它必然是素数，则 N 就等于，必会在最后加入 result，与假设矛盾。

5.素因子个数

1.朴素求法

还是试除法，我们套用优化枚举[1,\sqrt{n}]即可，时间复杂度O(\sqrt{n})

2.素数分解法

根据算数基本定理可得，n的因子一定是p_1,p_2...p_k的组合，而且例如p_1取得个数为[0,e_1]，p_2是[0,e_2]，以此类推。

由乘法原理可得，设总因子个数为g(n)，等于e_i+1的连乘，即表示如下

g(n)=\prod_{i=1}^{k}(e_i+1)

时间复杂度即求素因子分解的复杂度O(s)

6.GCD与LCM

1.模运算

对于一个正整数p，任意一个整数n，一定存在等式n=kp+r，其中k,r是整数，且0\le r<p，称k为n除以p的商，r为n除以p的余数，表示为n\,mod\,p =r

我们定义正整数和整数a,b满足如下运算

a\,mod\,p表示a除以p所得的余数

以下公式分别是模p加法，减法，乘法和幂模p

模运算满足结合律，交换律与分配律。

我们用a\equiv b\,(mod\,m)表示a与b模m意义下同余，说人话就是a和b除以m的余数相等

对于同余有如下性质

自反性：若a是整数，则a\equiv a\,(mod\, m)
对称性：若a和b是整数，且a\equiv b\,(mod\,m)，则b\equiv a\,(mod\,m)
传递性：若a,b,c是整数，且a\equiv b\,(mod\,m),b\equiv c\,(mod\,m)，则a\equiv c\,(mod\,m)。

关于同余的加减乘除，若a，b，c，d和m是整数，m>0，且a\equiv b\,(mod\,m),c\equiv d\,(mod\,m)

加：a+c\equiv b+d\,(mod\,m)
减：a-c\equiv b-d\,(mod\,m)
乘：ac\equiv bd\,(mod\,m)
除：在模的左右都同除一个数不能保证同余，后面会讲模除法

2.最大公约数

寻求最大公约数是人民民主的真谛...

由算数基本定理可得，有如下公式满足：

a=p_1^{x_1}p_2^{x_2}p_3^{x_3}...p_k^{x_k}
b=p_1^{y_1}p_2^{y_2}p_3^{y_3}...p_k^{y_k}

那么gcd(a,b)可以表示为以下形式，这个形式思考很好用！

gcd(a,b)=p_1^{min(x_1,y_1)}p_2^{min(x_2,y_2)}p_3^{min(x_3,y_3)}...p_k^{min(x_k,y_k)}

需要说明的是这里a和b的分解式中指数可以为0。

2.1 辗转相除法求最大公约数

当b\ne0时，我们令a=kb+r，其中k=\lfloor\frac{a}{b}\rfloor，r=a\,mod\,b，并且满足(0\le r<b)，当一个数c即使a的约数也是b的约数，那么则必然也是a-kb的约数，即r的约数。那么a和b的最大公约数=b和r的最大公约数。表示如下

gcd(a,b)=gcd(b,a\,mod\,b)

但是假设建立在b\ne0的情况下，而b=0的情况，答案显然为a，对于上述gcd函数，可以表示为如下递归式子。

gcd(a,b)=\begin{cases} a & b=0 \\ gcd(b,a\,mod\,b) & b\ne 0 \end{cases}

写成代码就是如下

int gcd(int a, int b) {

    return !b ? a : gcd(b, a % b);

}

也可以用std实现的std::__gcd(a,b)加下划线是不推荐使用因为没有安全保护，但毕竟我们又不是写多线程，直接用就完了。

gcd具有结合律，如下

gcd(a,b,c,d,e,f,g)=gcd(gcd(a,b),c,d,e,f,g)

P10463 Interval GCD

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r] 都加上 d。
Q l r，表示询问 A[l],A[l+1],…,A[r] 的最大公约数(GCD)。

显然线段树，根据gcd的结合律，我们可以进行暴力的单点修改，gcd根据结合律进行维护：

#include<bits/stdc++.h>

#define ll long long

#define ls p<<1

#define rs p<<1|1

#define gcd(a,b) __gcd(abs(a),abs(b))

#define pir pair<int,int>

using namespace std;

const int MN=5e5+15;

struct segtree

{

    int l,r;

    ll sum,d;

}t[MN<<2];

  

int n,m;

ll a[MN];

  

void pushup(int p){

    t[p].sum=t[ls].sum+t[rs].sum;

    t[p].d=gcd(t[ls].d,t[rs].d);

}

  
  

void build(int p,int l,int r){

    t[p].l=l;

    t[p].r=r;

    if(l==r){

        t[p].d=t[p].sum=a[l]-a[l-1];

        return;

    }

    int mid=l+r>>1;

    build(ls,l,mid);

    build(rs,mid+1,r);

    pushup(p);

}

  

void modify(int p,int x,ll k){

    if(t[p].l==t[p].r){

        t[p].sum+=k;

        t[p].d+=k;

        return;

    }

    int mid=t[p].l+t[p].r>>1;

    if(mid>=x) modify(ls,x,k);

    else modify(rs,x,k);

    pushup(p);

}

  

ll querys(int p,int fl,int fr){

    if(t[p].l>=fl&&t[p].r<=fr){

        return t[p].sum;

    }

    int mid=t[p].l+t[p].r>>1;

    ll ret=0;

    if(mid>=fl){

        ret+=querys(ls,fl,fr);

    }

    if(mid<fr){

        ret+=querys(rs,fl,fr);

    }

    return ret;

}

  

ll queryd(int p,int fl,int fr){

    if(t[p].l>=fl&&t[p].r<=fr){

        return t[p].d;

    }

    ll ret=0;

    int mid=t[p].l+t[p].r>>1;

    if(mid>=fl){

        ret=gcd(ret,queryd(ls,fl,fr));

    }

    if(mid<fr){

        ret=gcd(ret,queryd(rs,fl,fr));

    }

    return ret;

}

int main(){

    ios::sync_with_stdio(0);

    cin>>n>>m;

    for(int i=1;i<=n;i++){

        cin>>a[i];

    }

    char op;

    int l,r;

    ll v;

    build(1,1,n);

    while (m--)

    {

        cin>>op>>l>>r;

        if(op=='C'){

            cin>>v;

            modify(1,l,v);

            if(r!=n) modify(1,r+1,-v);

        }else{

            cout<<gcd(queryd(1,l+1,r),querys(1,1,l))<<'\n';

        }

    }

    return 0;

}

3.最小公倍数

两个数a和b的最小公倍数是指同时被a和b整除的最小倍数，记为lcm(a,b)。

特殊的，当a和b互素时，lcm(a,b)=ab

求LCM需要先求gcd，所以易得

lcm(a,b)=\frac{ab}{gcd(a,b)}

由算数唯一分解定理可得如下公式：

a=p_1^{x_1}p_2^{x_2}p_3^{x_3}...p_k^{x_k}
b=p_1^{y_1}p_2^{y_2}p_3^{y_3}...p_k^{y_k}

那么gcd(a,b)和lcm(a,b)可以表示为如下式子

gcd(a,b)=p_1^{min(x_1,y_1)}p_2^{min(x_2,y_2)}p_3^{min(x_3,y_3)}...p_k^{min(x_k,y_k)}
lcm(a,b)=p_1^{max(x_1,y_1)}p_2^{max(x_2,y_2)}p_3^{max(x_3,y_3)}...p_k^{max(x_k,y_k)}

需要说明的是这里a和b的分解式中指数可以为0。

我们将gcd和lcm相乘，由下列公式可得

min(x,y)+max(x,y)=x+y

可得lcm(a,b)\times gcd(a,b)=ab

等式两边同除gcd(a,b)

lcm(a,b)=\frac{ab}{gcd(a,b)}

代码如下

int lcm(int a, int b) {

    return a / gcd(a, b) * b;

}

7.拓展欧几里得定理——裴蜀定理

裴蜀定理是关于GCD的一个定理。

对于整数a和b，一定存在整数x,y使得ax+by=gcd(a,b)成立
推论：当a和b互素（即gcd(a,b)=1时）ax+by=1

或另一种形式

对于任意x,y，d=ax+by，d一定是gcd(a,b)的整数倍，最小的d就是gcd(a,b)，即可得ax+by=k\times gcd(a,b)\,\,(k \ge 1)

证明如下

例题： P4549 【模板】裴蜀定理

给定一个包含 n 个元素的整数序列 A，记作 A_1,A_2,A_3,...,A_n。

求另一个包含 n 个元素的待定整数序列 X，记 S=\sum\limits_{i=1}^nA_i\times X_i，使得 S>0 且 S 尽可能的小

我们可以发现，这个A_i\times X_i很类似于ax+by，并且这里的a和b给出了。这样A_i\times X_i就处理成了gcd(A_1,A_2)。

引理：gcd(a_1,a_2,...a_k)=gcd(gcd(a_1,a_2),gcd(a_3,a_4)...gcd(a_{k-1},a_k))

那么只需要合并结果就可以了

代码如下

#include<iostream>

#include<cmath>

#define ll long long

using namespace std;

ll gcd(ll x,ll y){

    if(y==0) return x;

    return gcd(y,x%y);

}

ll ans,awa;

int n;

int main(){

    cin>>n;

    cin>>ans;

    if(n==1){

        cout<<ans;

        return 0;

    }

    for(int i=2;i<=n;i++){

        cin>>awa;

        awa=abs(awa);

        ans=gcd(ans,awa);

    }

    cout<<ans;

    return 0;

}

8.线性同余方程——exgcd求解

exgcd拓展欧几里得算法

线性同余方程（也叫模线性方程）是最基本的同余方程，即 ax \equiv b(mod \ n)

其中 a、b、n 都为常量，x 是未知数，这个方程可以进行一定的转化，得到：ax = kn + b

这里的 k 为任意整数，于是我们可以得到更加一般的形式即：ax + by + c = 0

求解的第一步就是将原式化为ax+by=c 。

第二步求出d=gcd(a,b)，由裴蜀定理演变式可得如下式子

d(a \frac xd + b \frac yd) = c

容易知道(a \frac xd + b \frac yd)为整数，如果d不能整除c，则方程无解。

第三步：我们由2步可知方程有解则可以一定能表示成ax + by = c = gcd(a, b) \times c，那么如何求解呢，根据欧几里得定理有如下转化

\begin{aligned} d &= gcd(a, b) \\&= gcd(b, a\%b) & (1)\\&= bx' + (a\%b)y' & (2)\\&= bx' + [a-b \times \lfloor \frac ab \rfloor]y' & (3)\\&= ay' + b[x' - \lfloor \frac ab \rfloor y'] & (4)\end{aligned}

于是有\begin{cases}x &= y' \\ y &= x' - \lfloor \frac ab \rfloor y' \end{cases}

需要注意的是，当递归边界即b=1的情况下，此时易得x=1,y=0。

代码也就如下，这样吧x和y输进去，就得到了一组解

void exgcd(ll a,ll b,ll &x,ll &y){

    if(!b){

        x=1;

        y=0;

        return;

    }

    exgcd(b,a%b,y,x);

    y-=a/b*x;

}

例如求解方程27x+8y=1

点我观看动画！

例1：P1082 [NOIP2012 提高组] 同余方程

求关于 x 的同余方程 ax \equiv 1 \pmod {b} 的最小正整数解。

显然可以变化为ax+by=1，由裴蜀定理可得gcd(a,b)=1，a与b互素，通过exgcd我们能求出这个题的一组解，但是题目要求是最小正整数解，有可能求得的解为负数，也有可能过大。

对于原式ax+by=1，我们做如下变形

ax+by+k\times ba-k\times ba=1

a(x+kb)+b(y-ka)=1

即可得求出的解x由x_0+kb推得，所以我们可以对得出的结果做如下操作

ll a,b,x,y;

    cin>>a>>b;

    exgcd(a,b,x,y);

    cout<<(x%b+b)%b;

可以理解为加上b和减去b不会错过任何解

故AC代码如下，套板子就行

#include<iostream>

#define ll long long

using namespace std;

void exgcd(ll a,ll b,ll &x,ll &y){

    if(!b){

        x=1;

        y=0;

        return;

    }

    exgcd(b,a%b,y,x);

    y-=a/b*x;

}

int main(){

    ll a,b,x,y;

    cin>>a>>b;

    exgcd(a,b,x,y);

    cout<<(x%b+b)%b;

    return 0;

}

仔细看看这个题，是不是有点眼熟，我们把x替换为a^{-1}，我们发现这不就是在求模运算的逆元吗！

例题2：# P5656 【模板】二元一次不定方程 (exgcd)

要求输出ax+by=c中x和y的最小解和最大解,无解输出-1

有裴蜀定理可得，如果c不是gcd(a,b)的倍数，方程必定无解。

用exgcd求出ax_0+by_0=gcd(a,b)的整数解后，我们开始用这个特殊解取推ax+by=c的解，也就是求通解

由裴蜀定理推论得ax+by=k\times gcd(a,b)\,\,(k \ge 1)

所以可得ax+by=c变形为ax+by=k\times gcd(a,b)=c

k\times gcd(a,b)=c

k=\frac{c}{gcd(a,b)}

代入原式ax_0+by_0=gcd(a,b)

\frac{x_0c}{gcd(a,b)}a+\frac{x_0c}{gcd(a,b)}b=c

故可得x和y可以表示为

ax+by=c\,\begin{cases} x=x_0\times\frac{c}{gcd(a,b)} \\ y=y_0\times\frac{c}{gcd(a,b)} \end{cases}

既然我们用x_0和y_0表示了x和y，那我们就可以开始找出所有的解

我们开例1推的式子，我们将x_0和y_0分别代入x和y

不过我们换元求一下k

m=kb

n=ka

a(x_0+m)+b(y_0-n)=c

展开可得ax_0+by_0+am-bn=c

我们只需要让am-bn=0即可

设gcd(a,b)=d，我们让\begin{cases} m=t\times\frac{b}{d}\\n=t\times\frac{a}{d} \end{cases}

代入计算得\frac{ab}{d}-\frac{ab}{d}=0

这时候我们就证明了一个定理

由特殊解推到所有整数解的定理

设方程ax+by=c(其中a，b为非零整数)有一组整数解x=x_0,y=y_0，则方程的所有整数解可以表示为x=x_0+\frac{b}{gcd(a,b)}t，y=y_0-\frac{a}{gcd(a,b)}t

我们开始考虑最大最小值

\begin{cases} x=x_0+t\times\frac{b}{d}\\y=y_0-t\times\frac{a}{d} \end{cases}

我们可以发现当t增大的时候，x越来越大，y越来越小

由于增加减少的值太难写，我们考虑换元法。

令t_x=t\times\frac{b}{d}，t_y=t\times\frac{a}{d}

既然是正整数，那么即求x_{min}\ge1

代入上式可得

x_0+kt_x\ge1

变形即可得

k\ge\lceil\frac{1-x_0}{t_x}\rceil

为什么是上取整因为k必须大于这个值

可得x_{min}=x_0-\lceil\frac{1-x_0}{t_x}\rceil

x_min对应的y值正好就是y_{max}，若y_{max}<0 则无正整数解

懒的敲式子了

代码如下

#include<iostream>

#include<cmath>

#define ll long long

using namespace std;

int T;

ll exgcd(ll a,ll b,ll &x,ll &y){

    if(!b){

        x=1;

        y=0;

        return a;

    }

    ll d=exgcd(b,a%b,y,x);

    y-=a/b*x;

    return d;//这里求出的是gcd(a,b)

}

int main(){

    cin>>T;ll qp(ll a,ll b,ll mod){

    a%=mod;

    ll res=1;

    while(b>0){

        if(b&1){

            res=res*a%mod;

        }

        a=a*a%mod;

        b>>=1;

    }

    return res;

}

    while (T--)

    {

        ll a,b,c,x,y;

        cin>>a>>b>>c;

        ll d=exgcd(a,b,x,y);

        if(c%d!=0){//不能整除方程无解

            cout<<-1<<endl;

            continue;

        }

        x=x*c/d,y=y*c/d;//求x0和y0

        ll tx=b/d,ty=a/d;

        ll k=ceil((1.0-x)/tx);

        x+=tx*k;

        y-=ty*k;//求xmin和ymax

        if(y<=0){//如果ymax<0

            ll ansy=y+ty*(ll)1*ceil((1.0-y)/ty);

            cout<<x<<" "<<ansy<<endl;

        }else{

            cout<<(y-1)/ty+1<<" "<<x<<" "<<(y-1)%ty+1<<" "<<x+(y-1)/ty*tx<<" "<<y<<endl;

        }

    }

    return 0;

}

总结以下就是这个结论

9.快速幂

已知三个正整数a,b,c(a,b,c<=10^5) 求a^{b}\mod c

9.1 朴素算法

直接模拟一个b次的循环，枚举a对b次乘法

int f(int a, int b, int c) {

    int ans = 1;

    while(b--)

        ans = ans * a;

    return ans % c;

}

显然我们发现10^{10^5} 肯定在算的时候就炸INT了。

并且时间复杂度是O(b)的，时间复杂度不可以接受。

9.2 模乘

ab\mod c=(a\mod c)(b\mod c)\mod c

证明贴一个别人的

改进如下

int f(int a, int b, int c) {

    a = (a % c + c) % c;

    int ans = 1 % c;

    while(b--)

        ans = ans * a % c;

    return ans;

}

但是时间复杂度并没有改善。

9.3 二分快速幂

我们采用二分的思想，对原式进行分治法，有如下公式。

a^{b}\mod c=\begin{cases} 1\mod c & b为0\\a(a^{(b-1}{2})^{2}\mod c & b为奇数 \\ (a^{b/2})^2\mod c & b为偶数 \end{cases}

于是我们可以利用程序的递归思想，把函数描述成如下形式

f(a,b,c)=\begin{cases} 1\mod c & b为0\\ af(a,\frac{b-1}{2},c)^2 & b为奇数 \\ f(a,\frac{b}{2},c)^2 & b为偶数\end{cases}

代码如下：

ll qp(ll a,ll b,ll mod){

    a%=mod;

    ll res=1;

    while(b>0){

        if(b&1){

            res=res*a%mod;

        }

        a=a*a%mod;

        b>>=1;

    }

    return res;

}

注意如果乘法可能溢出，要使用龟速乘！

10.欧拉函数

对于正整数n，欧拉函数是小于等于n的正整数中与n互素的个数，记为\varphi(n) (其中\varphi(1)=1)

即\varphi(n)=\sum\limits_{i=1}^n[gcd(i,n)=1]

其中[A]表示当A成立时，[A]=1，反之[A]=0

对于素数p而言，小于等于p的数必然与他互素，故

\varphi(p)=p-1

对于素数的幂来说，有

\varphi(p^k)=p^k-p^{k-1}

对于素数p来说，有

\varphi(2p)=\varphi(p)

对于任意正整数n，有

n=\sum\limits_{d|n}\varphi(d)

对于任意两个互素的数p,q，他们乘积的欧拉函数如下

\varphi(pq)=\varphi(p)\times\varphi(q)

利用算数基本定理可得

故有任意正整数n，有

\varphi(n)=n\prod^k_{i=1}(1-\frac{1}{p_i})

单个数的欧拉函数求解

我们可以用定义来做，那么只需要枚举i，并求gcd(n,i)=1的满足个数。考虑算数唯一分解定理，和上面的一般式，我们可以枚举素数进行试除法

\varphi(n)=n\prod^k_{i=1}(\frac{p_i-1}{p_i})

当n=1的时候，返回1
当n>1，用ans来记录最终的欧拉函数值，初始值为n
- 对[2,\sqrt{n}]的素数进行试除，对于素数p，若满足p|n，则执行ans=ans/(\frac{i-1}{i})，n/=i把她质数次方因子筛没
当某个时刻n=1的时候直接返回ans的值。若试除完后还有剩余说明n是一个素数，返回ans/(\frac{n-1}{n})

代码如下

int phi(int n){

    int ans=n;

    for(int i=2;i*i<=n;i++){

        if(n%i==0){

            ans=ans/i*(i-1);

            while (n%i==0)

            {

                n/=i;

            }

        }

    }

    if(n>=2){

        ans=ans/n*(n-1);

    }

    return ans;

}

先除后乘防止超Int范围

欧拉筛

因为欧拉函数是积性函数，\varphi(xy)=\varphi(x)\varphi(y)

可得如下筛法，时间复杂度O(n)

phi[1]=1;

    for(int i=2;i<=n;i++)

    {

        if(!vis[i]) p[++cnt]=i,phi[i]=i-1;//质数只有自身与自己不互质

        for(int j=1;p[j]&&i*p[j]<=n;j++)

        {

            vis[i*p[j]]=1;

            if(!(i%p[j]))

            {

                phi[i*p[j]]=phi[i]*p[j];

                //这里是平方因子了，不要减1

                break;

            }

            else phi[i*p[j]]=phi[i]*(p[j]-1);//第一次出现因子，乘p-1

        }

    }

11.积性函数

数论函数指定义域为正整数的函数。

若数论函数 f 满足当 \gcd(a,b)=1 且f(1)=1时 f(ab)=f(a)f(b)，则 f 为积性函数。

若数论函数 f 满足任何正整数 a,b 有 f(ab)=f(a)f(b)，则 f 为完全积性函数。

一些积性函数

单位函数 \epsilon(n)=[n=1]（完全积性）
常函数 1(n)=1（完全积性）
幂函数 I_k(n)=n^k
恒等函数 \mathrm{id}(n)=n，\mathrm{id}_k(n)=n^k（完全积性）
因数和函数 \sigma(n)=\sum_{d|n}d，\sigma_k(n)=\sum_{d|n}d^k
约数个数d(n)=\sigma_0(n)=\sum_{d|n}1

1-1e18的函数取值对照表

经典永流传~

例题：CF920F

给定n个数的数组a，m次操作，操作有2种(1 \le n,m \ge 3\times 10^5,1\le a_{i}\le 10^6)

将i \in [l,r]中所有a_i替换为d(a_i)

求\sum\limits_{i=l}^{r}a_i

这里阐述一个估算d(x)的方法

对于任意正整数x，一定有d(x)\le \sqrt{3x}
对于x>1260，一定有d(x)<\sqrt{x}

那么这个题很好做，不难根据表发现当a_i=10^6,d(a_i)=240。线段树维护，单点暴力修改，注意要打tag来保持复杂度。

故有代码：

#include<bits/stdc++.h>

#define ls p<<1

#define rs p<<1|1

#define ll long long

using namespace std;

const int MN=3e5+15,MA=1e6+15;

template<typename type>

inline void read(type &x)

{

    x=0;bool flag(0);char ch=getchar();

    while(!isdigit(ch)) flag=ch=='-',ch=getchar();

    while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();

    flag?x=-x:0;

}

struct segtree{

    int l,r;

    bool isok;

    ll sum;

}t[MN<<2];

ll a[MN];

int n,m;

  

//https://wenku.baidu.com/view/9e336795bb4cf7ec4afed057.html?_wkts_=1739964897460&needWelcomeRecommand=1

//对于任意正整数n,有d(n)<=sqrt(3*n)

//对于n>1260，有d(n)<sqrt(n)

  

//d是约数个数，时间复杂度线性筛O(n)

// num是最小素因子个数，用于筛约数

int d[MA],num[MA];

vector<bool> vis(MA);

vector<int> prime;

  

void pushup(int p){

    t[p].sum=t[ls].sum+t[rs].sum;

    if(t[ls].isok==1&&t[rs].isok==1){

        t[p].isok=1;

    }

}

  

void build(int p,int l,int r){

    t[p].l=l;

    t[p].r=r;

    if(l==r){

        t[p].sum=a[l];

        if(t[p].sum==1||t[p].sum==2){

            t[p].isok=1;

        }

        return;

    }

    int mid=l+r>>1;

    build(ls,l,mid);

    build(rs,mid+1,r);

    pushup(p);

}

  

void update(int p,int fl,int fr){

    if(t[p].isok) return;

    if(t[p].l==t[p].r){

        t[p].sum=d[t[p].sum];

        if(t[p].sum==1||t[p].sum==2) t[p].isok=1;

        return;

    }

    int mid=t[p].l+t[p].r>>1;

    if(mid>=fl) update(ls,fl,fr);

    if(mid<fr) update(rs,fl,fr);

    pushup(p);

}

  

ll query(int p,int fl,int fr){

    if(t[p].l>=fl&&t[p].r<=fr){

        return t[p].sum;

    }

    ll ret=0;

    int mid=t[p].l+t[p].r>>1;

    if(mid>=fl)ret+=query(ls,fl,fr);

    if(mid<fr) ret+=query(rs,fl,fr);

    return ret;

}

  

void getd(){

    d[1]=1;

    for(int i=2;i<MA;i++){

        if(!vis[i]){

            prime.push_back(i);

            d[i]=2;

            num[i]=1;

        }

        for(int j=0;1ll*i*prime[j]<MA&&j<prime.size();j++){

            vis[i*prime[j]]=1;

            if(i%prime[j]==0){

                num[i*prime[j]]=num[i]+1;

                d[i*prime[j]]=d[i]/(num[i]+1)*(num[i*prime[j]]+1);

                break;

            }else{

                d[i*prime[j]]=d[i]*2;

                num[i*prime[j]]=1;

            }

        }

    }

}

  

int main(){

    ios::sync_with_stdio(0);

    getd();

    read(n);

    read(m);

    for(int i=1;i<=n;i++){

        read(a[i]);

    }

    int op,x,y;

    build(1,1,n);

    while (m--)

    {

        read(op);

        read(x);

        read(y);

        if(op==1){

            update(1,x,y);

        }else{

            cout<<query(1,x,y)<<'\n';

        }

    }  

}

12.欧拉定理与费马小定理

12.1 欧拉定理

n和a为正整数，且n,a互素，则a^{\varphi(n)} \equiv 1(\mod n)

证明？

推论：

若正整数 a,b 互质则满足 a^x \equiv 1 \pmod b 的最小正整数解 x_0 是 \varphi(b) 的约数

可以用欧拉定理反证法证明。

例题：洛谷P1463_POI_2001_HAOI_2007_反素数

12.2 费马小定理

若p为素数，gcd(a,p)=1，则a^{p-1}\equiv 1(\mod p)
对于任意整数a，有a^p\equiv a(\mod p)

12.2.1 判定素数

我们回到判定素数的那一节，如果我们要判定的范围超过的10^{12}，那么就无法使用O(\sqrt{n})的算法来求解。

我们可以用费马小定理，随机找几个和n互素的a。

计算a^{n-1} \mod n

若结果均为1，那么认为n，是一个素数。这样的时间复杂度O(Clog_2n)，常数C表示找C个a来测试。

但是，以上假设不成立！

因为在费马小定理的条件中，若置换条件。

若a^{p-1}\equiv 1(\mod p)，不能推导出p是素数

例如561，这一类数我们称其为伪素数，又称为卡迈克尔数，在 n\le 10^9 内有 255 个。

若 n 为卡迈克尔数，则 2^n-1 也是卡迈克尔数，故其个数是无穷的。

12.2.2 Miller_Rabin算法

Miller Rabin素性检验是一种素数判定的法则，由CMU的教授Miller首次提出，并由希大的Rabin教授作出修改，变成了今天竞赛人广泛使用的一种算法，故称Miller Rabin素性检验。

本质其实是随机化算法，能在时间复杂度为 O(C \log^3 n) 的情况下判断（这里 C 同上），但是具有一定错误概率，但是在 OI 范围内能保证步出错。

既然我们单纯费马小定理无法判断，我们只好引入新的定理来提高我们的正确性。

二次探测定理：对于质数 p，若 x^2 \equiv 1 \pmod p，则小于 p 的解只有两个，x_1=1,x_2=p-1。

证明：

\begin{aligned} x^2 & \equiv 1 \pmod p \\ x^{2}-1 & \equiv 0 \pmod p \\ (x+1)(x-1) & \equiv 0 \pmod p \\ p &| (x+1)(x-1) \\ \\ \because &p \text{是质数} \\ \\ \therefore &\begin{cases} x_1=1 \\ x_{2}= p-1\\ \end{cases} \end{aligned}

这个定理有什么用？

如果费马小定理检测得到 a^{p-1} \equiv 1 \pmod p，并且 p-1 为偶数（否则 p 为偶数直接被筛了），则 a^{p-1} 相当于 x^2。

拆分为 \left(a^{\dfrac{p-1}{2}}\right)^2 \equiv 1 \pmod p，可以用二次检测定理判断。

如果 a^{\frac{p-1}{2}} 在 \pmod p 的情况下的解不是 1 或者 p-1，那么 p 就不是素数。

如果 \left(a^{\frac{p-1}{2}}\right)^2 \equiv 1 \pmod p，可以模仿之前操作在进行一次检验，变判断 a^{\frac{p-1}{4}}，不断执行直到为计数。

也就是说，我们可以将 p-1=u\times 2^t，其中 u 为奇数。对于 a^u,a^{u\times 2},a^{u \times 2^2} \dots这一系列数进行检验，他们的解要么是 1 要么出现 p-1 后全是 1 （前面不能出现1），否则就不是素数，当然要注意 p-1 不能出现在最后一个数否则不满足费马小定理，还要注意过程中不能产生 p 的倍数。

过程如下：

先特判 3 以下的数和偶数
将 n-1 化为 u\times 2^t。
选取多个底数 a，对 a^u,a^{u\times 2},a^{u \times 2^2} \dots进行检验，判断解是否全为 1，或在非最后一个数的情况下出现 p-1。
如果都满足，则认为为素数。

板子题：SP288——PON

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr ll prime[]={2,3,5,7,11,13,17,37};

ll qmul(ll a,ll b,ll MOD){
    ll ret=0;
    while(b){
        if(b&1) ret=(ret+a)%MOD;
        b>>=1;
        a=(a+a)%MOD;
    }
    return ret;
}

ll qpow(ll a,ll b,ll MOD){
    ll ret=1;
    while(b){
        if(b&1) ret=qmul(ret,a,MOD);
        a=qmul(a,a,MOD);
        b>>=1;
    }
    return ret;
}

bool MillerRabin(ll n){
    if(n<3||n%2==0) return n==2;
    ll d=n-1,tot=0;
    while(d%2==0) d/=2,++tot;
    for(auto p:prime){
        ll v=qpow(p,d,n);
        if(v==1||v==n-1||v==0) continue;
        for(int j=1;j<=tot;j++){
            v=qmul(v,v,n);
            if(v==n-1&&j!=tot){
                v=1;
                break;
            }
            if(v==1) return 0;
        }
        if(v!=1) return 0;
    }
    return 1;
}

int main(){
    int T;
    cin>>T;
    while(T--){
        ll n;
        cin>>n;
        cout<<(MillerRabin(n)?"YES\n":"NO\n");
    }
    return 0;
}

12.2.2 二分快速幂降幂

给出一个大整数n(1\le n \le 10^{100000})

求2^n\mod 1e9+7

令x=p-1，由费马小定理得

2^{p-1}\mod p=1

m=n\mod(p-1) 可以用大数取余求解，求得的m \in [0,p-1)，再利用快速幂求解即可。

12.3 拓展欧拉定理

说到这里，我们先来看看欧拉定理的局限性

欧拉定理：

n和a为正整数，且n,a互素，则a^{\varphi(n)} \equiv 1(\mod n)

不难发现，局限性在于互素，即gcd(a,n)=1，那么如果不互素，怎么办？这时候就要用到“拓展欧拉定理”了

拓展欧拉定理如下：

定义：

a^b \equiv \begin{cases} a^{(b \mod \varphi(m))} & gcd(a,m)=1 \\ a^b & gcd(a,m) \ne 1,b< \varphi(m) \\ a^{((b+\varphi(\,mod \,\varphi(m))} & gcd(a,m)\ne 1,(b\ge \varphi(m) \end{cases} \quad (mod\,\,\,\,m)

其中第二行的意思，若gcd(a,m) \ne 1,b< \varphi(m)那么是不能降幂的。

题目中的m不会太大，但是如果b<\varphi(m)，复杂度可以用快速幂求解，但是大于那么就会问题，所以就要靠降幂来实现。

证明略（啊？）

应用：

12.3.1 拓展欧拉定理的应用

P5091 【模板】扩展欧拉定理

求a^b \mod m

其中1\le a\le 10^9,1\le b\le10^{20000000},1\le m \le 10^8

十分甚至九分的恐怖，甚至都没有互素，直接套上去看看。

\varphi(x)可以用线性筛求得，但是b过大，我们可以用边读入边取余的方式。

代码？

#include<iostream>

#define ll long long

using namespace std;

int phi(int n){

    int ans=n;

    for(int i=2;i*i<=n;i++){

        if(n%i==0){

            ans=ans/i*(i-1);

            while (n%i==0)

            {

                n/=i;

            }

        }

    }

    if(n>=2){

        ans=ans/n*(n-1);

    }

    return ans;

}

inline int read(int mod)

{

    int x=0;

    bool g=false;

    char c=getchar();

    while(c<'0'||c>'9') c=getchar();

    while(c>='0'&&c<='9')

    {

        x=(x<<3)+(x<<1)+(c^'0');

        if(x>=mod) x%=mod,g=true;//判断是否大于哦啦函数

        c=getchar();

    }

    if(g) return (x+mod);

    else return x;

}

ll quickpow(ll a,ll b,ll mod){

    ll ret=1;

    while (b)

    {

        if (b&1){

            ret=ret*a%mod;

        }

        a=a*a%mod;

        b>>=1;

    }

    return ret%mod;

}

int main(){

    ll a,mod,cishu;

    cin>>a>>mod;

    cishu=read(phi(mod));

    cout<<quickpow(a,cishu,mod);

    return 0;

}

13.逆元与线性同余方程

定义：

形如

ax \equiv b \,\,\, (mod \,m)

的方程称为线性同余方程，其中a,b,m均已知，但是x未知。从[0,m-1]中求解x，x不唯一需求出全体解。

13.1 逆元求解

逆元可以理解为模意义下的除法，符号为a^{-1}（暴论）

可以理解为倒数eee，然而实际上不是倒数，人家就叫做逆元。

考虑最简单的情况，gcd(a,m)=1即互素时，可以计算a的逆元，并将方程两边乘以a的逆元，得到唯一解。

线性方程组解的数量等于gcd(a,n)或等于0（即无解）

13.2 拓展欧几里得算法求解

我们可以将取余的式子改写为如下的形式：

ax+ny=b

不难发现可以用拓展欧几里得算法求解该方程，得一组解，在通过之前上面讲过的单一解求通解，在拓展到全体解，即可得到。

其实说实话这两个不是一种东西吗...

其实是等价的。

例题：

P1082 [NOIP2012 提高组] 同余方程

求关于 x 的同余方程 ax \equiv 1 \pmod {b} 的最小正整数解。

不是这个题怎么又上来了？

然而实际上这个题刚好就能作为例题eee

代码重放

#include<iostream>

#define ll long long

using namespace std;

void exgcd(ll a,ll b,ll &x,ll &y){

    if(!b){

        x=1;

        y=0;

        return;

    }

    exgcd(b,a%b,y,x);

    y-=a/b*x;

}

int main(){

    ll a,b,x,y;

    cin>>a>>b;

    exgcd(a,b,x,y);

    cout<<(x%b+b)%b;

    return 0;

}

13.3 快速幂求解逆元

乘法逆元就是求\frac{a}{b} \mod p=a\times x \mod p中的x。

那么也就是说\frac{a}{b} \equiv a\times x \,\text{(mod p)}

那么有1\equiv b\times x \,\text{(mod p)}

由费马小定理可得当p为质数时逆元为x=b^{(p-2)}

快速幂即可求解。

13.4 阶乘逆元O(n)

留存一份，一般是先exgcd或快速幂求解f[n]，让后倒序递推，一定注意开long long！

jc[0] = 1;

    for (int i = 1; i <= 1e5; i++)

    {

        jc[i] = (i * jc[i - 1]) % MOD;

    }

    ll x, y;

    inv[100000] = binpow(jc[100000], MOD - 2);

    for (int i = 100000 - 1; i >= 0; i--)

    {

        inv[i] = inv[i + 1] * (i + 1) % MOD;

    }

14.线性同余方程组——中国剩余定理（EXTRA！）

「物不知数」问题：有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

答：我不会，我不会，我不会，啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊┗( T﹏T )┛

14.1 中国剩余定理

中国剩余定理可以求解如下的一元线性同余方程组。

\begin{cases} x\equiv a_{1} \mod n_{1}\\ x\equiv a_{2} \mod n_{2} \\ \space \space \space\ \ \vdots \\ x\equiv a_{n} \mod n_{k}\end{cases}

其中n_1,n_{2} \ldots n_{k}两两互质

方法：

计算所有模数的积：n
对于第i个方程：
- 计算m_i=\frac{n}{n_i}
- 计算m_i在模n_i意义下的逆元m_i^{-1}
- 计算c_i=m_{i}* m_i^{-1} (不要取模！)
方程组在模n意义下的唯一解为$$
x=\sum\limits_{i=1}^k a_ic_i

P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪

实现代码如下：

#include<iostream>

#define ll long long

using namespace std;

const int MN=1e5+15;

int a[MN],b[MN],n;

ll mt=1;

ll exgcd(ll a,ll b,ll &x,ll &y){

    if(!b){

        x=1;

        y=0;

        return a;

    }

    ll d=exgcd(b,a%b,y,x);

    y-=a/b*x;

    return d;

}

ll inv(ll a,ll n){

    ll x,y;

    exgcd(a,n,x,y);

    return (x%n+n)%n;

}

long long quick_mul(long long x,long long y,long long mod)

{

    long long ans=0;

    while(y!=0){

        if(y&1==1)ans+=x,ans%=mod;

        x=x+x,x%=mod;

        y>>=1;

    }

    return ans;

}

ll crt(){

    ll ans=0;

    for(int i=1;i<=n;i++){

        ll m=mt/a[i],invm=inv(m,a[i]);//exgcd求逆元

        ll ci=m*invm;

        ans=(ans+quick_mul(b[i],ci,mt))%mt;//使用龟速乘

    }

    return (ans%mt+mt)%mt;

}

int main(){

    cin>>n;

    for(int i=1;i<=n;i++){

        cin>>a[i]>>b[i];

        mt*=a[i];

    }

    cout<<crt();

    return 0;

}

14.2 EXCRT拓展中国剩余定理

\begin{cases} x\equiv a_{1} \mod n_{1}\\ x\equiv a_{2} \mod n_{2} \\ \space \space \space\ \ \vdots \\ x\equiv a_{n} \mod n_{k}\end{cases}

其中n_1,n_{2} \ldots n_{k}两两互质，这样我们当然是可以用CRT来解决的，但是如果不互质怎么办？就需要用到拓展中国剩余定理。

与中国剩余定理的区别在哪里？在于我们需要合并方程才能做，例如合并上面两个式子：

x\equiv a_{1} \mod n_{1}

x \equiv a_{2}\mod n_2

合并为：x\equiv a' \mod (n_1n_{2}/ gcd(m_1,m_2))

若合并了所有方程，那么得到的解即为最终解。

证明：

根据方程可变形为：

x\equiv a_1+n_1y_1

x\equiv a_2+n_2y_2

可得：a_1+n_1y_1=a_2+n_2y_{2}\Rightarrow n_1y_1-m_2y_2=a_2-a_1

转换为经典的ax+by=c的格式，先用exgcd求出ax+by=gcd(a,b)的解。

通过上面变形过的方程够再出一个\mod m_1m_2/gcd(m_1,m_2)的解

即得证。

代码如下：

#include<iostream>

#define ll long long

using namespace std;

const int MN=1e5+15;

ll md[MN],b[MN],mt; // md数组存储模数，b数组存储余数，mt未使用

int n; // 同余方程的数量

  

// 慢速乘法：计算 (a*b) % mod，使用快速乘法算法避免溢出

ll slowti(ll a,ll b,ll mod){

    ll ret=0;

    while (b>0)

    {

        if(b&1) ret=(ret+a)%mod; // 如果b的最低位是1，累加a

        a=(a+a)%mod; // a乘以2

        b>>=1; // b右移一位

    }

    return ret;

}

  

// 扩展欧几里得算法：解ax + by = gcd(a,b)

ll exgcd(ll a,ll b,ll &x,ll &y){

    if(!b){

        x=1; // 基础情况处理

        y=0;

        return a; // 返回gcd

    }

    // 递归调用，交换x和y的位置

    ll ret=exgcd(b,a%b,y,x);

    y-=a/b*x; // 更新y的值

    return ret;

}

  

// 扩展中国剩余定理(EXCRT)：求解同余方程组

ll excrt(){

    ll x,y; // 用于存储exgcd的解

    ll m1=md[1],b1=b[1]; // 初始化第一个方程

    ll ans=(b1%m1+m1)%m1; // 初始解

    for(int i=2;i<=n;i++){

        ll m2=md[i],b2=b[i]; // 当前方程的模数和余数

        // 合并方程为 m1*x ≡ (b2-b1) mod m2

        ll a=m1,b=m2,c=(b2-b1%m2+m2)%m2; // c = (b2-b1) mod m2

        // 求解方程 a*x + b*y = c

        ll d=exgcd(a,b,x,y); // d是gcd(a,b)

        // 如果c不能被d整除，无解

        if(c%d!=0){

            return -1;

        }

        // 调整x的解

        x=slowti(x,c/d,b/d);

        // 计算新的解

        ans=b1+x*m1;

        // 更新模数为lcm(m1,m2) = m1*m2/d

        m1=m2/d*m1;

        // 确保解在模m1意义下最小非负

        ans=(ans%m1+m1)%m1;

        // 更新b1为当前解

        b1=ans;

    }

    return ans;

}

  

int main(){

    cin>>n; // 输入同余方程的数量

    for(int i=1;i<=n;i++){

        cin>>md[i]>>b[i]; // 输入每个方程的模数和余数

    }

    cout<<excrt(); // 输出解

    return 0;

}

15.数论分块

15.1 数论分块引入

求\sum\limits_{i=1}^n \lfloor \frac{n}{i} \rfloor，其中n\le 10^{12}

第一眼看上去是不可做题，因为如果我们直接暴力枚举的话是肯定不行的，因为我们枚举到10^9就做不动了，这个时候就要清楚数论分块。

我们比如果举例一个函数，比如果y=\frac{15}{x}罢，他的函数图像如下：

我们根据题意，把他的下取整表示出来（图中红色）：

有没有发现什么，发现对应的下取整都是一个横线端（~~这不废话吗~~)，而且是分成一小段一小段的。

或者我们搬一个图来举例（出处vvauted的数论分块)：

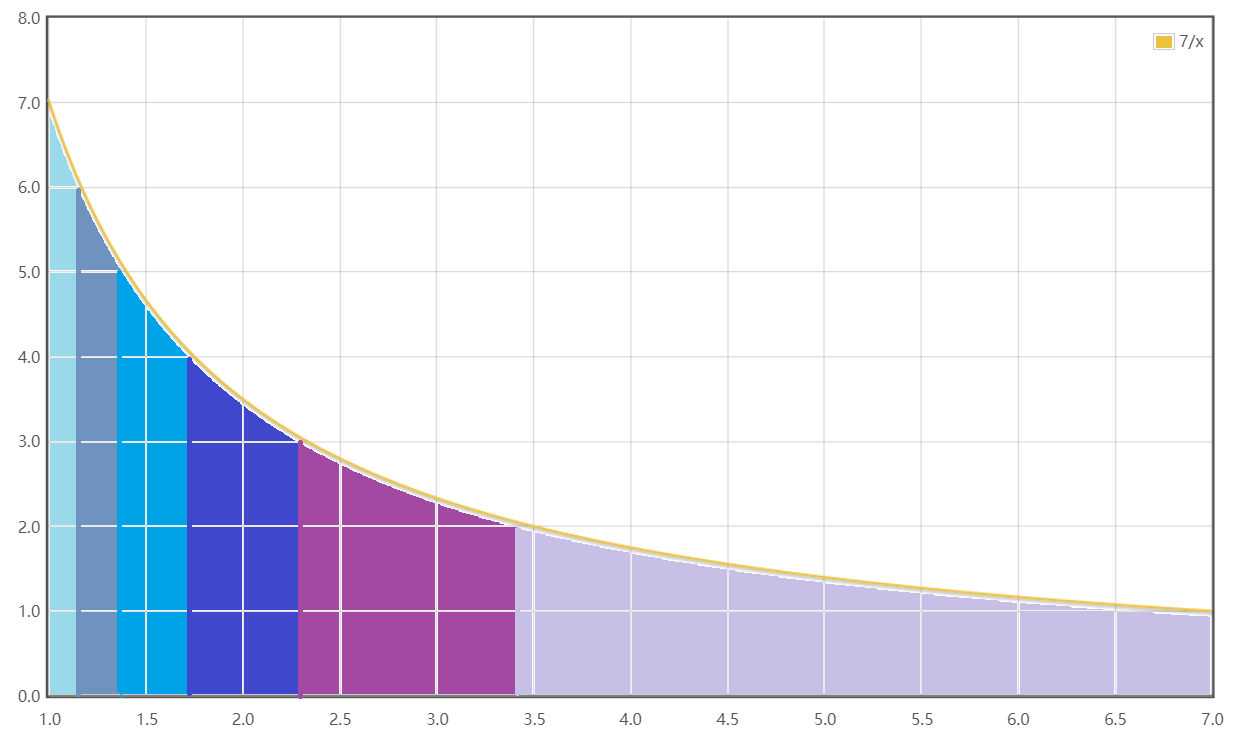
没错，数论分块中的分块就是看中的这一点,图像中是被分割成了几个大块，只要我们不断枚举块，就能显著的降低时间复杂度！

但是问题在于我们怎么知道每个块的右端点？这里给出一个引理。

对于任意一个i，其最大的满足\lfloor \frac{n}{i} \rfloor=\lfloor \frac{n}{j} \rfloor的 j 满足：

j=\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor

证明如下：

\lfloor \frac{n}{i} \rfloor \le \frac{n}{i}

\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor \ge \lfloor \frac{n}{\frac{n}{i}}\rfloor

\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor \ge i

得证。

复杂度分析：

当x\in[1,\lfloor \sqrt{n} \rfloor]的区间时最多有\lfloor \sqrt{n} \rfloor个取值

当x\in[\lfloor \sqrt{n} \rfloor,n]同理仍最多有\lfloor \sqrt{n} \rfloor个取值。

共2\lfloor \sqrt{n} \rfloor的值，时间复杂度即O(\sqrt{n})

15.2.1 例题1：约数研究

求\sum\limits_{i=1}^{n}f(i)，其中n\le 10^6

f(i)即i的约束个数

对于i，我们在[1,n]中的约数个数就是\lfloor \frac{n}{i} \rfloor，那么原命题转化为：

\sum\limits_{i=1}^n f(i)=\sum\limits_{i=1}^n \lfloor \frac{n}{i} \rfloor

那么其实可以直接O(n)暴力就可以了，所以说吗这个题难度其实是个橙题。

但是如果n\le 10^{14}呢？那么就可以数论分块楼。

我们考虑一个块怎么贡献，根据式子，其实就是(r-l+1)\times \lfloor \frac{n}{i} \rfloor。

那么代码也就如下：

#include<bits/stdc++.h>

#define ll long long

using namespace std;

int main(){

    ll n,ans=0;

    cin>>n;

    for(ll i=1,j;i<=n;i=j+1){

        j=n/(n/i);

        ans+=(j-i+1)*(n/i);

    }

    cout<<ans;

    return 0;

}

15.2.2 余数求和

给定n,k，求：\sum\limits_{i=1}^n k \mod n
n,k\le 10^9

这个题很有数论分块的感觉，毕竟这已经不能O(n),必须出分块！

简单转换一下，把取模变成如下式子：

\sum\limits_{i=1}^{n} k-\lfloor \frac{k}{i} \rfloor \times i

=n\times k - \sum\limits_{i=1}^n \lfloor \frac{k}{i} \rfloor \times i

直接数论分块就可以了，但是这个我们再算贡献的时候与\sum\limits_{i=l}^r i，需要等差数列一下。

那么代码如下：

#include<bits/stdc++.h>

#define ll long long

using namespace std;

ll n,k,ret=0;

ll getsum(ll l,ll r){

    if(r>n) r=n;

    return (r-l+1)*(l+r)/2;

}

  

int main(){

    cin>>n>>k;

    ret+=n*k;

    for(ll i=1,j;i<=n;i=j+1){

        if(k/i==0) break;

        j=k/(k/i);

        if(j>n) j=n;

        ret-=(k/i)*getsum(i,j);

    }

    cout<<ret;

    return 0;

}

15.2.3 约数求和PLUS

定义f(n)=\sum\limits_{i|n} i，给定x,y求区间[x,y]的f和

x,y \le 10^9

简单的拆成两个前缀和的形式，现在只需要求出[1,n]的答案怎么求，可以想到转化成如下式子：

\sum\limits_{i=1}^n f(i)=\sum\limits_{i=1}^n\sum\limits_{k|i} k

交换一下求和顺序：

\sum\limits_{k=1}^n\sum\limits_{k|i}k(k\le n)

不难发现转化为了约数为k的数的前缀和，那么直接做就可以了。即为\sum\limits_{k=1}^{n} k\times \lfloor \frac{n}{k} \rfloor

那么直接写就没了。。。代码如下：

#include<bits/stdc++.h>

#define ll long long

using namespace std;

ll n,m;

  

ll getsum(ll l,ll r){

    return (r-l+1)*(l+r)/2;

}

  

int main(){

    cin>>n>>m;

    n--;

    ll retn=0,retm=0;

    for(ll i=1,j;i<=n;i=j+1){

        j=n/(n/i);

        retn+=(n/i)*getsum(i,j);

    }

    for(ll i=1,j;i<=m;i=j+1){

        j=m/(m/i);

        retm+=(m/i)*getsum(i,j);

    }

    cout<<retm-retn;

    return 0;

}

这个只是属于一个工具，如果考这个复杂度是显然可以观察出来的，往下取整的式子推就可以了。

16.狄利克雷卷积

证明一般可能省略或给出。

狄利克雷卷积，是定义在数论函数间的一种二元运算，有如下两个等价定义：

(f*g)(n)=\sum\limits_{xy=n}f(x)g(y)

或如下等价式：

(f*g)(n)=\sum\limits_{d|n}f(d)g(\frac{n}{d})

积性函数之间的狄利克雷卷积有一个重要的性质：

若f,g是积性函数，那么f*g也是积性函数。

证明如下：

显然有(f*g)(1)=f(1)g(1)=1，我们不妨设a,b互质，有：

(f*g)(a)=\sum\limits_{d|a}f(d)g(\frac{a}{d}),(f*g)(b)=\sum\limits_{d|b}f(d)g(\frac{b}{d})

(f*g)(ab)=\sum\limits_{d|ab}f(d)g(\frac{ab}{d})

注意到：

\begin{align} \sum\limits_{d|a}f(d)g(\frac{a}{d}) \cdot \sum\limits_{d|b}f(d)g(\frac{b}{d}) & = \sum\limits_{d_1|a,d_2|b}f(d_1)g(\frac{a}{d_1}) \cdot f(d_2)g(\frac{b}{d_2})\\ \sum\limits_{d|a}f(d)g(\frac{a}{d}) \cdot \sum\limits_{d|b}f(d)g(\frac{b}{d}) & = \sum\limits_{d_1|a,d_2|b}f(d_1d_2)g(\frac{ab}{d_1d_2}) \end{align}

因为a,b互质，那么ab的因数可以唯一的表示a,b的某个因数。

那么若f,g是积性函数，那么f*g也是积性函数这一结论得证，同时我们也证明了如下式子：

(f*g)(a) \cdot (f*g)(b) =(f*g)(ab)

16.1 除数函数与幂函数

根据定义有(f*1)(n)=\sum\limits_{d|n}f(d)1(\frac{n}{d})=\sum\limits_{d|n}f(d)

所以得：

(Id_k * 1)(n) =\sum\limits_{d|n} Id_k(d) =\sum\limits_{d|n} d^k = \sigma _k

16.2 欧拉函数与恒等函数

因为：

(\varphi * 1)(n)=\sum\limits_{d|n} \varphi(d)

当d=p^m时（p为质数），有：

\sum\limits_{d|n} \varphi(d) =\varphi(1)+\sum\limits_{i=1}^m \varphi(p^i) = p^m = d

那么可得(\varphi * 1)(p^m)=p^m

那么现在设n为任意正整数时，由算数唯一分解定理，并且(\varphi * 1)(p^m)显然为积性函数，那么根据算数唯一分解定理，因为带入一个质数的任意方仍和原值相同，那么带入之后其实和带入之前是一模一样的，即：

(\varphi * 1)(\Pi p^m)=\Pi (\varphi * 1)(p^m)=\Pi p^m

即得：

(\varphi * 1)(n)=n

\varphi * 1 =Id

16.3 单位函数e与莫比乌斯函数\mu

有如下关系式：

e=\mu*1=\sum\limits_{d|n}\mu(d)

证明利用单位元（下面）性质即可，略。

16.4 狄利克雷卷积的性质

接下来我们来阐述狄利克雷卷积的一些性质：

具有交换性:(f*g)(n)=(g*f)(n)
具有结合律:((f*g)*h)(n)=(f*(g*h))(n)
对函数加法的分配率:(f*(g+h))(n)=(f*g)(n)+(f*h)(n)

单位元：

(\varepsilon * f)(n)=\sum\limits_{d|n}\varepsilon(d)f(\frac{n}{d})=f(n)

故单位函数即为狄利克雷卷积的单位元。

逆元：

假设f*g=\varepsilon，我们称g为f的狄利克雷逆元，记为f^{-1}。

f存在狄利克雷卷积的必要条件是f(1)\neq 0

f^{-1}是积性函数。

对于证明过程可以去网上找，这里就不在叙述了。

17.莫比乌斯函数及反演

17.1 莫比乌斯函数的小性质

对于莫比乌斯函数的定义我们这里不在详细叙述，需要去积性函数那里找。

莫比乌斯函数是积性函数，于是我们可以用线性筛来筛！

代码如下：

vector<bool> vis(MN);
vector<ll> prime;
ll n,mu[MN];

void euler(){
    vis[1]=1;
    mu[1]=1;
    for(int i=2;i<=n;i++){
        if(!vis[i]){
            prime.push_back(i);
            mu[i]=-1;
        }
        for(auto p:prime){
            if(i*p>n) break;
            vis[p*i]=1;
            if(i%p==0){
                mu[i*p]=0;
                break;
            }
            mu[i*p]=-mu[i];
        }
    }
}

莫比乌斯函数还具有另一个性质：

\sum\limits_{d|n}\mu(d)=[n=1]

证明需用到组合计数，这里就不在叙述了。

那么我们就能根据推论得到一个反演常用的结论：

\sum\limits_{d|gcd(i,j)}\mu(d)=[gcd(i,j)=1]

但是到现在我们还并没有说反演到底是啥，我们下面就来说。

17.2 莫比乌斯反演

设f(n),g(n)为两个数论函数。

如果有：

f(n)=(g*1)(n)=\sum\limits_{d|n}g(d)

那么有：

g(n)=(\mu * f)(n)=\sum\limits_{d|n}\mu(d) f(\frac{n}{d})

证明运用卷积即可。

17.3 对于一类求和式

有如下式子：

\sum\limits_{i=1}^{n}\sum\limits_{j=1}^mf(gcd(i,j))

一般套路：

我们可以尝试构造出函数g，使得有如下式子：

f=(g*1)=\sum\limits_{d|n}g(d)

不难替换：

\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|gcd(i,j)}g(d)

\sum\limits_{d=1}g(d)\sum\limits_{i=1}^n [d|i]\sum\limits_{j=1}^m [d|j]

不难发现后面两项就是在枚举约数个数，可以转化为\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor

最终式为：

\sum\limits_{d=1}g(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor

即得，数论分块求解即可。

17.4 小例题

例1.1 :

\sum\limits_{i=1}^n\sum\limits_{j=1}^mgcd(i,j)

不难发现其实就是Id(gcd(i,j))，利用16.2学到的性质，那么就直接发现是欧拉函数，结束。

\sum\limits_{d=1}\varphi(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor

例1.2:

\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=1]

不难发现是单位函数e，那么根据16.3结束。

\sum\limits_{d=1}\mu(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor

例2:

\sum\limits_{x=a}^b\sum\limits_{y=c}^d [gcd(x,y)=k]

其中1\le a,b,c,d,k\le 5\times 10^4

这种区间，我们可以套路的转化为前缀和的形式，用容斥原理求解，那么不难转化：

f(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=k]

考虑把k给提出来，有：

\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}[gcd(i,j)=1]

套入例1.2

\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}\sum\limits_{d|gcd(i,j)}\mu(d)

考虑下取整的式子能否直接代入，其实是可以的。那么有

\sum\limits_{d=1}\mu(d)\lfloor\frac{n}{kd}\rfloor\lfloor\frac{m}{kd}\rfloor

线性筛求\mu让后整除分块即可，瓶颈在线性筛，时间复杂度O(n)

例3:
P3768 简单的数学题

\sum\limits_{i=1}^n\sum\limits_{j=1}^n(ij*gcd(i,j)) \mod m

上来发现式子有点不像人样，尝试枚举gcd，有：

\sum\limits_{d=1}d\sum\limits_{i=1}^n\sum\limits_{j=1}^nij[gcd(i,j)=d]

我们发现这个式子和例2及其详细，我们可以转化过去，但是注意ij\rightarrow id*jd，我们不能一步转化

\sum\limits_{d=1}d\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{k}\rfloor}[gcd(i,j)=1]*id*jd

考虑把d提出来

\sum\limits_{d=1}d^3\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{k}\rfloor}[gcd(i,j)=1]*ij

现在把例二丢进去：

\sum\limits_{d=1}d^3\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{k}\rfloor}ij\sum\limits_{k|gcd(i,j)}\mu(k)

如果我们想转化成最终形式，我们考虑ij的贡献，其实只是在运算的时候把求和式子中的1变了ij，那么不难有。

\sum\limits_{d=1}d^3\sum\limits_{k=1}\mu(k)k^2\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{kd}\rfloor}ij

有没有发现多了个k^2，是因为你的ij如果都提出来（指求和里的分母kd）里面都有一个k，那么提出来就要k^2

考虑后面式子，后面式子我们其实可以O(1)计算，有：

f(\lfloor\frac{n}{kd}\rfloor,\lfloor\frac{m}{kd}\rfloor)=\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}i\sum\limits_{j=1}^{\lfloor\frac{n}{kd}\rfloor}j=\frac{\lfloor\frac{n}{kd}\rfloor\times(\lfloor\frac{n}{kd}\rfloor+1)}{2}\times\frac{\lfloor\frac{m}{kd}\rfloor\times(\lfloor\frac{m}{kd}\rfloor+1)}{2}

考虑前面的式子，发现枚举没有上界或者上界很大，我们能不能限制上界？

发现分式中的kd可以换元，并且换元的上界在n，考虑换元为t=kd。

考虑枚举d，让后k能够求出来：

\sum\limits_{t=1}^n\sum\limits_{d|t}d^3\mu(\frac{t}{d})(\frac{t}{d})^2f(\lfloor\frac{n}{t}\rfloor,\lfloor\frac{n}{t}\rfloor)

考虑把立方和平方消去：

\sum\limits_{t=1}^nt^2f(\lfloor\frac{n}{t}\rfloor,\lfloor\frac{n}{t}\rfloor)\sum\limits_{d|t}d\mu(\frac{t}{d})

后面的式子其实就是\sum\limits_{d|n}Id(d)\mu(T)=\varphi(t),反演得到。

不难有：

\sum\limits_{t=1}^{n}t^2\varphi(t)f(\lfloor\frac{n}{t}\rfloor,\lfloor\frac{n}{t}\rfloor)

到这里我们完成80%，不难发现后面O(1)可以求，对于前面，数论函数前缀和，考虑杜教筛。

原式为\sum\limits_{i=1}^nId_2(i)\varphi(i)

我们需要构造函数g使得：

\sum\limits_{d|n}Id_2(d)\varphi(d)g(\frac{n}{d})

能够快速求出。

考虑直接把Id_2砍了

令g=Id_2

那么原式Id_2拆开：

\sum\limits_{d|n}d^2\varphi(d)(\frac{n}{d})^2=n^2\sum\limits_{d|n}\varphi(d)=n^3

最后一个式子考虑反演变为Id

那么这道题做完了，不难发现g可以快速预处理，时间复杂度O(n)。

代码如下：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN = 2e6 + 15;
ll inv2, inv6, P, n, fsum[MN + 15], phi[MN + 15];
unordered_map<ll, ll> ump;
vector<bool> vis(MN + 15);
vector<ll> prm;

inline ll read()
{
    ll x = 0, t = 1;
    char ch = getchar();
    while ((ch < '0' || ch > '9') && ch != '-')
        ch = getchar();
    if (ch == '-')
        t = -1, ch = getchar();
    while (ch <= '9' && ch >= '0')
        x = x * 10 + ch - 48, ch = getchar();
    return x * t;
}

ll ksm(ll a, ll b)
{
    ll ret = 1;
    while (b)
    {
        if (b & 1)
        {
            ret = (ret * a) % P;
        }
        a = a * a % P;
        b >>= 1;
    }
    return ret;
}

ll getlf(ll k)
{
    k %= P;
    return ((k * (k + 1) % P * inv2 % P) * (k * (k + 1) % P * inv2 % P)) % P;
}

ll getpf(ll k)
{
    k %= P;
    return (k * (k + 1) % P * (2 * k + 1) % P * inv6 % P) % P;
}

void getphi()
{
    vis[0] = vis[1] = 1;
    phi[1] = 1;
    for (ll i = 2; i <= MN; i++)
    {
        if (!vis[i])
        {
            prm.push_back(i);
            phi[i] = i - 1;
        }
        for (auto p : prm)
        {
            if (p * i > MN)
                break;
            vis[p * i] = 1;
            if (i % p == 0)
            {
                phi[i * p] = phi[i] * p;
                break;
            }
            else
                phi[i * p] = phi[i] * (p - 1);
        }
    }
    for (ll i = 1; i <= MN; i++)
    {
        fsum[i] = (fsum[i - 1] + i * i * phi[i] % P) % P;
    }
}

ll dushu(ll k)
{
    if (k <= MN)
        return fsum[k];
    if (ump[k])
        return ump[k];
    ll ans = getlf(k), now, pre;
    for (ll i = 2, j; i <= k; i = j + 1)
    {
        j = k / (k / i);
        ans = (ans - (getpf(j) - getpf(i - 1)) % P * dushu(k / i) % P) % P;
    }
    return ump[k] = (ans + P) % P;
}

ll solve()
{
    ll ans = 0, pre = 0, now;
    for (ll i = 1, j; i <= n; i = j + 1)
    {
        j = n / (n / i);
        now = dushu(j);
        ans = (ans + ((now - pre) * getlf(n / i)) % P) % P;
        pre = now;
    }
    return (ans + P) % P;
}

int main()
{
    P = read();
    n = read();
    getphi();
    inv6 = ksm(6, P - 2);
    inv2 = ksm(2, P - 2);
    cout << solve();
    return 0;
}

18. 二项式反演

18.1 定义及转化

~~真服了好多次模拟赛考这个自己都不会转化导致就只能在那里坐牢。~~

二项式反演用于解决 “某个物品恰好若干个” 这一类计数例题。

我们记 f_n 表示恰好使用 n 个有标号的元素形成特定结构的方案数，g_n 表示从 n 个有标号的元素中选出 i(i\ge 0) 个元素形成特定结构的总方案数。

若已知 g_n，需要求解 f_i，那么有如下反演公式。

f_n=\sum\limits_{i=0}^n \binom{n}{i} (-1)^{n-i} g_i

证明过程如下：

\begin{aligned} f_n&=\sum\limits_{i=0}^n \binom{n}{i}(-1)^{n-i}g_{i}\\ f_n&=\sum\limits_{i=0}^n \binom{n}{i}(-1)^{n-i} \left[ \sum\limits_{j=0}^i \binom{i}{j}f_{j} \right]\\ f_n&=\sum\limits_{i=0}^n\sum\limits_{j=0}^i \binom{n}{i} \binom{i}{j} (-1)^{n-i} f_j \end{aligned}

考虑交换求和顺序，为了满足 j\le i，交换后对于 j 需要满足大于等于它的 i。

\begin{aligned} f_n&=\sum\limits_{i=0}^n\sum\limits_{j=0}^i \binom{n}{i} \binom{i}{j} (-1)^{n-i} f_j \\ & = \sum\limits_{j=0}^nf_{j}\sum\limits_{i=j}^n \binom{n}{i} \binom{i}{j} (-1)^{n-i} \\ \\ & \because \binom{n}{i}\binom{i}{j}=\binom{n}{j}\binom{n-j}{i-j} \\ & \therefore \sum\limits_{j=0}^nf_{j}\sum\limits_{i=j}^n \binom{n}{j} \binom{n-j}{i-j} (-1)^{n-i} \\ \\ & =\sum\limits_{j=0}^n \binom{n}{j} f_{j}\sum\limits_{i=j}^n \binom{n-j}{i-j} (-1)^{n-i} \\ \end{aligned}

设 k=i-j , \because i\in [j,n] , \therefore k\in [0,n-j]。

\begin{aligned} f_n&=\sum\limits_{j=0}^n \binom{n}{j} f_{j}\sum\limits_{i=j}^n \binom{n-j}{i-j} (-1)^{n-i} \\ &=\sum\limits_{j=0}^n \binom{n}{j} f_{j}\sum\limits_{k=0}^{n-j} \binom{n-j}{k} (-1)^{n-j-k} \\ & \because \sum\limits_{i=0}^n (-1)^{n-i}\binom{n}{i}=[n=0] \\ \\ \therefore f_n&=\sum\limits_{i=0}^n \binom{n}{j}f_{j}[n-j=0] \\ & = \sum\limits_{i=0}^n \binom{n}{j}f_{j}[n=j] \\ & =f_{n}\\ \\ & \because f_n=f_{n}\\ & \therefore \text{得证} \end{aligned}

而做题过程中往往遇见的是 g_n 好求而 f_n 却不好求。

那么二项式反演就是干这个的，利用 g_n 去求 f_n。

18.2 二项式反演形式总结

形式1:

g_n 表示至多 n 个/种的方案数量，f_n 恰好 n 个/种方案数量。

g_n=\sum\limits_{i=0}^n \binom{n}{i} f_{i}\Leftrightarrow f_{n}= \sum\limits_{i=0}^n (-1)^{n-i} \binom{n}{i} g_i

形式2:

g_k 表示至少 k 个/种的方案数量，f_k 恰好 k 个/种方案数量。

g_k=\sum\limits_{i=k}^n \binom{i}{k} f_{i}\Leftrightarrow f_{k}= \sum\limits_{i=0}^n (-1)^{i-k} \binom{i}{k} g_i

18.3 例题

洛谷P9850
[ICPC 2021 Nanjing R] Ancient Magic Circle in Teyvat

给定 n 个点的完全图，其中 m 条边为红色边，其余边为蓝色边。
定义以下：
f_{\text{红色}} 为四元组 (i,j,k,l)，其中任意两点都有红色边连接的个数。
f_{\text{蓝色}} 为四元组 (i,j,k,l)，其中任意两点都有蓝色边连接的个数。
求 |f_{\text{红色}}-f_{\text{蓝色}}|。
其中 1\le n \le 10^5,1\le m \le 2\times 10^5。

赛时没想出正解（废话都没学二项式反演能做？）

发现蓝色很难受，显然可以考虑以下容斥，但是怎么容斥呢？
红色边的信息我们是有的，我们可以通过红色边来容斥。

但是这咋求啊？暴力枚举直接 O(n^4) 了www。

对于一张存在 j 条红色边的图，假设存在 g_i 个 i 条边的红色子图，而且只需要满足边颜色都是红色就可以了，那么有 \binom{j}{i} 种选择方法，那么我们不妨设 f_i 表示四元组存在 i 条边的红色子图个数，有下列式子：

g_i=\sum\limits_{j=i}\binom{j}{i} f_j

长的就很二项式反演：

f_i=\sum\limits_{j=i}\binom{j}{i} (-1)^{j-i} g_j

那么 |f_6-f_0|=|g_0-g_1+g_2-g_3+g_4-g_5|。不难发现可以一个一个讨论（废话那你怎么求）

g_0：不选红色边，瞎选4个点：\dbinom{n}{4}。
g_1:选一个的方案数 \dbinom{m}{1}，让后在确定2个端点瞎选：\dbinom{m}{1}\dbinom{n-2}{2}。
g_2：分类讨论
- 如果是一点连两条边，枚举公共点，让后再枚举以该端点出发的两个点，让后再瞎选一个：(n-3)\sum\limits_{i=1}^{n}\dbinom{deg_i}{2}，其中 deg_i 表示节点 i 的度数
- 如果没有公共点，正南则反，就是原图任意选2个边减去有公共点的，即：\dbinom{m}{2}-\sum\limits_{i=1}^n \dbinom{deg_i}{2}。
g_3：继续
- 如果三元环，那就枚举剩下一个点为 (n-3)C_3.
- 如果是共用一个顶点，那么很简单直接枚举即可，结果 \sum\limits_{i=1}^n \binom{n}{3}。
- 如果是链，注意一下要把三元环的三个情况舍去，结果就是 \sum\limits_{(u,v)\in E}(deg_u-1)(deg_v-1)-3C_3。
g_4:
- 如果四元环，那不用枚举直接 C_4.
- 如果三元环出来一个那就是 \sum\limits_{i=1}^n T_i(deg_i-2)，其中 T_i 为 i 号点不同三元环的个数
g_5 ：只能是两个三元环共用一条边枚举公共边即可，其中 f_5=\sum\limits_{i=\in \mathbb{C}_3}\binom{t_i}{2} ，其中 \mathbb{C}_3 表示求解三元环完成定向的边集，t_i 表示覆盖带边 i 的不同三元环个数。

做完了，直接公式计算即可，注意瓶颈在三元环和四员化计算，不要超过 O(n^2)：

#include <bits/stdc++.h>
#define pir pair<int, int>
#define ll long long
using namespace std;
constexpr int MN = 1e5 + 15, MM = 2e5 + 15;
struct Edge {
    int u, v;
} e[MM];
ll f0, f1, f2, f3, f4, f5;
int dg[MN],n,m,top,s[MN],id[MN];
ll cp[MN], ce[MM];
vector<int> adj[MN];
vector<pir> G[MN];

ll countthree() {
    ll ret = 0;
    for (int i = 1; i <= n; i++) {
        for (auto p : G[i]) id[p.first] = p.second;
        for (auto p : G[i]) {
            int v = p.first;
            for (auto pv : G[v]) {
                int w = pv.first;
                if (id[w]) {
                    ret++;
                    cp[i]++;
                    cp[v]++;
                    cp[w]++;
                    ce[p.second]++;
                    ce[pv.second]++;
                    ce[id[w]]++;
                }
            }
        }
        for (auto p : G[i]) id[p.first] = 0;
    }
    return ret;
}

ll countfour() {
    memset(id, 0, sizeof(id));
    ll ret = 0;
    for (int i = 1; i <= n; i++) {
        for (int v : adj[i]) {
            for (auto p : G[v]) {
                int w = p.first;
                if (dg[i] < dg[w] || (dg[i] == dg[w] && i < w)) {
                    ret += id[w];
                    if (!id[w]) s[++top] = w;
                    id[w]++;
                }
            }
        }
        for (int j = 1; j <= top; j++) id[s[j]] = 0;
        top = 0;
    }
    return ret;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> e[i].u >> e[i].v;
        dg[e[i].u]++;
        dg[e[i].v]++;
        adj[e[i].u].push_back(e[i].v);
        adj[e[i].v].push_back(e[i].u);
    }

    for (int i = 1; i <= m; i++) {
        int u = e[i].u, v = e[i].v;
        if ((dg[u] == dg[v] && u > v) || dg[u] > dg[v])
            swap(u, v);
        G[u].push_back({v, i});
    }

    ll tri = countthree();
    ll quad = countfour();

    for (int i = 1; i <= n; i++) {
        f2+=1LL * dg[i] * (dg[i] - 1) / 2 * (n - 4);
        f3+=1LL * dg[i] * (dg[i] - 1) * (dg[i] - 2) / 6;
        f4+=1LL * cp[i] * (dg[i] - 2);
        for (auto p : G[i]) {
            int v = p.first;
            f3+=1LL * (dg[i] - 1) * (dg[v] - 1);
        }
    }

    for (int i = 1; i <= m; i++) {
        f5+=1LL * ce[i] * (ce[i] - 1) / 2;
    }

    f0=(__int128)n * (n - 1) * (n - 2) * (n - 3) / 24;
    f1=1LL * m * (n - 2) * (n - 3) / 2;
    f2+=1LL * m * (m - 1) / 2;
    f3+=tri * (n - 6);
    f4+=quad;
    cout << abs(f0 - f1 + f2 - f3 + f4 - f5);
    return 0;
}

19. 威尔逊定理

这个定理真的很冷门的……

威尔逊定理给定了判断某个自然是是否是素数的一个充分必要条件。

对于自然数 n>1，当且仅当 n 是素数时，(n-1)! \equiv -1 \pmod n。

逆定理：若 (p-1)! \equiv -1 \pmod p，则 p 是质数。

证明？

19.1 证明

首先需要说明的是，我们的前提是 n>1,n \in \mathbb{Z}。

我们把非素数分成几类：

\text{非素数} \begin{cases} 4 \\ \text{大于}4 \begin{cases} \text{完全平方数} \\ \text{非完全平方数} \end{cases} \end{cases}

显然这样分类保证不重不漏

19.1.1 充分性

当 n=4 时，代入有 (4-1)! \equiv 2 \pmod 4 ,不成立。

当 n 为完全平方数，则 p=k^2，因为 p>4 那么有 k>2。

让后我们比较 2k,p 之间的大小。

\begin{aligned} 2k-p & = 2k-k^2 \\ & = 2k-k^2-1+1 \\ & = -(k-1)^2+1<0 \end{aligned}

推论既得

\begin{aligned} &\because k<p,2k<p \\ & \therefore (p-1)! \\ & = 1\times 2 \times \dots \times k \times 2k\times \dots \times (p-1) \\ & =k \times 2k \times n \\ & = 2nk^2 \\ & = 2np \\ & \therefore (p-1)! \equiv 0 \pmod p \end{aligned}

若 p 不是完全平方数，那么 p 必然等于两个完全不相等的数 a 和 b 的乘积，不妨设 a<b，满足：1<a<b<p。

显然有：

\begin{aligned} (p-1)! & =1\times 2\times \dots \times a\times b \times \dots \times (p-1) \\ & = a\times b\times n \\ & = nab \\ & =np \\ & \therefore (p-1)! \equiv 0 \pmod p \end{aligned}

19.1.2 必要性

当 p 为素数，考虑二次探测定理：

二次探测定理：对于质数 p，若 x^2 \equiv 1 \pmod p，则小于 p 的解只有两个，x_1=1,x_2=p-1。

再对于 a\in [2,p-2]，必然存在一个和它不相登的逆元 a^{-1} \in [2,p-2]，满足

aa^{-1} \equiv 1 \pmod p

所以必然有 \frac{p-3}{2} 对数相乘的乘积为 1，即：

(p-2)! \equiv 1 \pmod p

两边同乘 p-1，注意到 (-1+p) \mod p 不就是经典的负数取模吗，直接游戏结束。

(p-1)! \equiv -1 \pmod p

19.2例题

广义问题

对于 2\le n \le 10^9，求

(n-1)! \mod n

建议看证明。

配合素数判定

UVA1434 YAPTCHA

求下列式子答案：

\sum\limits_{k=1}^n \lfloor \frac{(3k+6)!+1}{3k+7} -\lfloor \frac{(3k+6!)}{3k+7} \rfloor \rfloor

我们对于上面定理变个形式：

(n-1)!+1\equiv 0 \pmod n

到这里你回看上面这个式子，是不是直接就秒了。

别急，我们分类讨论：

当 k 为质数，显然 \dfrac{(3k+6)!+1}{3k+7} 这个式子是整除式子，得到的是整数，而对于后面的式子不难想出来下取整为一定比前面式子小，但两者之差绝对值不会不是 1 （有疑惑自行举例自己想）。
当 k 不为质数，显然 \dfrac{(3k+6)!+1}{3k+7} 得到为的数就不是整除式子其结果就大于 0 了，而且还不是整数，而对于后面的式子呢？其实他们下取证的结果是一样的，差1不会影响。所以得到的结果为0

源命题转化为，统计素数问题，线性筛即可。

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=3e6+100;
int T,cnt[MN];


vector<bool> notprime(MN+5),isprime(MN+15);

vector<int> prime;

void shai(int n){
    for(int i=2;i<=n;i++){
        if(!notprime[i]){
            isprime[i]=1;
            prime.push_back(i);
        }
        for(auto p:prime){
            if(i*p>n) break;
            notprime[i*p]=1;
            if(i%p==0) break;
        }
    }
}

int main(){
    shai(3e6+15);
    for(int i=1;i<=1e6;i++){
        cnt[i]=cnt[i-1]+isprime[3*i+7];
    }
    cin>>T;
    while (T--)
    {
        int x;
        cin>>x;
        cout<<cnt[x]<<'\n';
    }
    
    return 0;
}

20.BSGS 与 exBSGS

补天坑

我们能够解决线性同余方程，这很好，我们来解决高级一点的——高次同余方程。

高次同余方程，有 a^x \equiv b \pmod p 和 x^a \equiv b \pmod p 这两个形式，其中 x 均为未知数，前面就是我们要讲的 BSGS，而后面就是我们大名鼎鼎的原根，这里我们讨论BSGS。

20.1 BSGS

问题：

给定整数 a,b,p，其中 a,p 互质，求 a^x \equiv b \pmod p 的非负整数解。

因为 a,p 互质，我们可以在模 p 意义下瞎搞乘除运算。

暴力做法

当然我们可以暴力枚举 x 计算，根据欧拉定理我们给出推论这个 x 是 O(\varphi(p)) 级别的，暴力枚举即可。

BSGS

虽然 O(\varphi(p)) 的枚举可以解决这个问题，但是性能肯定不行，我们需要一个更优雅的暴力来解决这个问题。

什么，优雅的暴力？~~那不就是分块吗。~~

我们不妨把待求的 x 分解以下，给定一个 A，那么就能分解成 x=mA-n 的形式，原式为：

\begin{aligned} a^{mA-n} & \equiv b \pmod p \\ a^{mA} & \equiv ba^{n} \pmod p \end{aligned}

显然这里的 n 应该不大于 A,m\le \lceil \frac{p}{A} \rceil。

我们考虑暴力枚举每一个 n ，把 ba^n \mod p 的值用哈希表存起来让后再枚举每一个 m 判断 a^{mA} \mod p 在哈希表中有没有对应的元素。

枚举 n 的复杂度为 O(A)，枚举 m 的复杂度为 O(\frac{p}{A})。

注意到 A+\frac{n}{A}，当 A=\sqrt{n} 时取最小值，复杂度即为优秀的 O(\sqrt{n})。

所以为什么是大步小步呢，你看 a^n 枚举 n 是小小的枚举 a 的指数，而 a^{mA} 是以 a^A 的指数一大步一大步枚举，所以形象的称为大步小步算法。

代码如下,实现因为用了 map 所以多一个 \log ：

map<int,int> mp; // 注意爆long long!

int BSGS(int a,int b,int p){
    mp.clear();
    b%=p;
    int t=sqrt(p)+1;
    for(int j=0;j<t;j++){
        int val=(long long)b*qpow(a,j,p)%p;
        mp[val]=j;
    }
    a=qpow(a,t,p);
    if(a==0) return b==0?1:-1;
    for(int i=0;i<t;i++){
        int val=qpow(a,i,p);
        int j=mp.find(val)==mp.end()?-1:mp[val];
        if(j>=0&&i*t-j>=0) return i*t-j;
    }
    return -1;
}

20.2 exBSGS

就和拓展中国剩余定理一样，我们这里的拓展就是不互质的情况下，那怎么做？

注意到，我们当然互质不能做（废话），我们考虑怎么改写。

咱们可以换成求解线性同余方程的形式，变形为：

a^x +kp =n

当 \gcd(a,n)|n 时有解，否则无解（裴蜀定理）。

由特殊解推一般解公式（还是裴蜀定理那里）得：

a^{x-1} \cdot \frac{a}{d} + k \cdot \frac{p}{d}=\frac{n}{d}

考虑重新传参，一直递归直到 \gcd(a,p)=1，让后做正常的 BSGS。

不妨设递归了 cnt 次，那么所有次递归的 d 的乘积我们设为 d'。

原式即为：

a^{x-cnt} \cdot \frac{a^{cnt}}{d'} \equiv \frac{n}{d'} \pmod{\frac{p}{d'}}

此时互质，BSGS即可，当然结果要加上 cnt ，那么代码如下。

int qpow(int a,int b,int MOD){
    int ret=1;
    while(b){
        if(b&1){
            ret=ret*a%MOD;
        }
        a=a*a%MOD;
        b>>=1;
    }
    return ret;
}

int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}

int BSGS(int a,int b,int p){
    mp.clear(); // 记得换unordered_map
    b%=p;
    int t=sqrt(p)+1;
    for(int j=0;j<t;j++){
        int val=b*qpow(a,j,p)%p;
        mp[val]=j;
    }
    a=qpow(a,t,p);
    if(a==0) return b==0?1:-1;
    for(int i=0;i<=t;i++){
        int val=qpow(a,i,p);
        int j=mp.find(val)==mp.end()?-1:mp[val];
        if(j>=0&&i*t-j>=0) return i*t-j;
    }
    return -1;
}

int exBSGS(int a,int b,int p){
    a%=p,b%=p;// 战术取余，因为以及是转线性同余可以这样做
    if(b==1||p==1) return 0;
    int gcdd,d=1,cnt=0,x,y;
    while((gcdd=exgcd(a,p,x,y))^1){
        if(b%gcdd) return -1;// 如果无解
        b/=gcdd,p/=gcdd;
        cnt++;
        d=1ll*d*(a/gcdd)%p; // 累计d
        if(d==b) return cnt; // 如果已经有解
    }

    exgcd(d,p,x,y); // 战术求逆元
    int inv=(x%p+p)%p;
    b=1ll*b*inv%p;
    int ans=BSGS(a,b,p);
    if(ans==-1) return -1; // 特别注意不要写错！
    else return ans+cnt;
}

Share

0.前言

1.扬帆启航——整除

1.任意性

2.传递性

3.可消性

4.组合性

2.数论的基础——素数

1.素数的定义

2.素数判定

3.素数筛法

1.埃式筛

2.欧拉筛（线性筛）

3.算数唯一分解定理

4.素因子分解

5.素因子个数

1.朴素求法

2.素数分解法

6.GCD与LCM

1.模运算

2.最大公约数

2.1 辗转相除法求最大公约数

3.最小公倍数

7.拓展欧几里得定理——裴蜀定理

8.线性同余方程——exgcd求解

exgcd拓展欧几里得算法

由特殊解推到所有整数解的定理

9.快速幂

9.1 朴素算法

9.2 模乘

9.3 二分快速幂

10.欧拉函数

单个数的欧拉函数求解

欧拉筛

11.积性函数

一些积性函数

1-1e18的函数取值对照表

12.欧拉定理与费马小定理

12.1 欧拉定理

12.2 费马小定理

12.2.1 判定素数

12.2.2 Miller_Rabin算法

12.2.2 二分快速幂降幂

12.3 拓展欧拉定理

12.3.1 拓展欧拉定理的应用

13.逆元与线性同余方程

13.1 逆元求解

13.2 拓展欧几里得算法求解

13.3 快速幂求解逆元

13.4 阶乘逆元O(n)

14.线性同余方程组——中国剩余定理（EXTRA！）

14.1 中国剩余定理

14.2 EXCRT拓展中国剩余定理

15.数论分块

15.1 数论分块引入

15.2.1 例题1： 约数研究

15.2.2 余数求和

15.2.3 约数求和PLUS

16.狄利克雷卷积

16.1 除数函数与幂函数

16.2 欧拉函数与恒等函数

16.3 单位函数e与莫比乌斯函数\mu

16.4 狄利克雷卷积的性质

17.莫比乌斯函数及反演

17.1 莫比乌斯函数的小性质

17.2 莫比乌斯反演

17.3 对于一类求和式

17.4 小例题

18. 二项式反演

18.1 定义及转化

18.2 二项式反演形式总结

18.3 例题

19. 威尔逊定理

19.1 证明

19.1.1 充分性

19.1.2 必要性

19.2例题

广义问题

配合素数判定

20.BSGS 与 exBSGS

15.2.1 例题1：约数研究