Kruskal 重构树

说实话，这个东西还是过于冷门了，感觉刷题练这个真心没啥用。

什么是 Kruskal 重构树

对于一张无向图，我们可以通过 Kruskal 算法求出其最小/最大生成树。

在求最小/最大生成树的时候，设两点 x、y 连边，则新建一个节点 p，连接到 x、y，将 p 的权值设为原边的权值。即用一个点替换了原本应该连接的边。

这是原图：

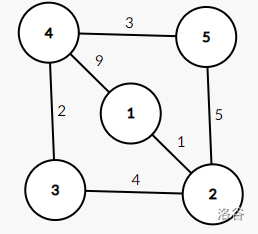
找到它的最小生成树：

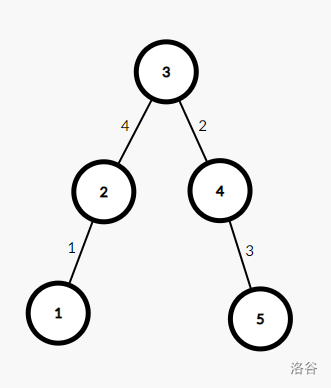
按边权从小到大建立 Kruskal 重构树：

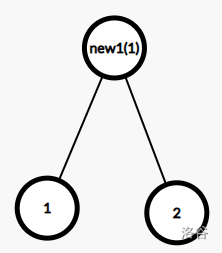
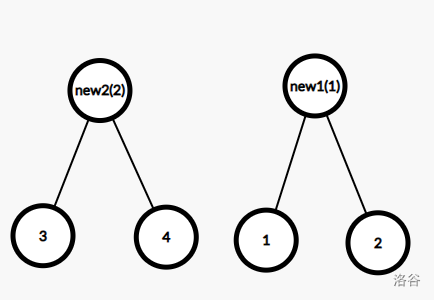
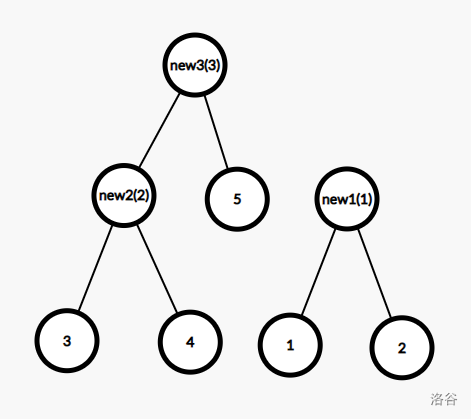
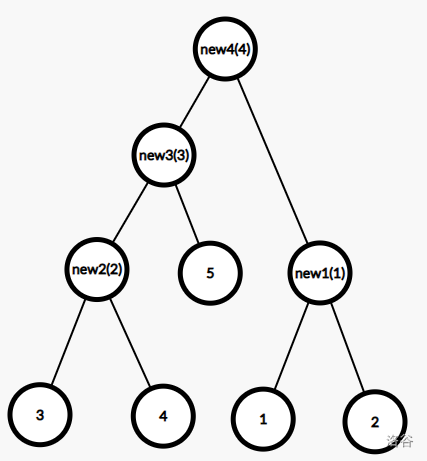
Kruskal 重构树的性质

1. 这是一颗二叉树。
2. 按最小生成树建立就是大根堆，反之。
3. 所有叶子节点是真实存在的点，非叶子节点是虚拟节点。
4. 原图中，x、y 之间所有路径的最大边权的最小值，是最小生成树上两点路径间的最大边权，也是 Kruskal 重构树上两点的 LCA（最近公共祖先）。

Kruskal 的基本 trick

Kruskal 最简单的应用就是直接求解最大边权最小值/最小边权最大值。

Kruskal 的进阶 trick

在 Kruskal 中，任何一个非叶子节点都可以被视为一种“瓶颈”，即如果 LCA 作为瓶颈如果没有被限制，则其子树一定没有被限制。通过这一点，引申出了许多 Kruskal 重构树的应用。

参考代码

void Kruskal(){
    sort(s+1,s+m+1,cmp);

    cnt=n;

    for(int i=1;i<=m;i++){
        int x=s[i].x,y=s[i].y,k=s[i].k;
        x=kru.find(x),y=kru.find(y);

        if(x==y) continue;

        cnt++;
        add(x,cnt),add(y,cnt);
        val[cnt]=k;
        kru.merge(x,cnt);
        kru.merge(y,cnt);
    }
}

例题

P1967 [NOIP 2013 提高组] 货车运输 - 洛谷

这是最简单的应用，一眼就能看出其要求是求出最小边权最大值。

应该建立最大生成树时建立重构树，然后求出 LCA。

注意本题图可能不连通，需要分开处理 LCA。

参考代码（Kruskal 重构树+Tarjan LCA）。

复杂度瓶颈在于排序，为 O(n \log n)。

P2245 星际导航 - 洛谷

同样是最简单的应用，这回要求求出最大边权最小值。

和上题相同，只是变成了建立最小生成树。

可以用此题继续熟练。

P9638 「yyOI R1」youyou 的军训 - 洛谷

Kruskal 重构树本身可以作为“瓶颈”一类的限制。

可以考虑建立一颗最大边权的 Kruskal 重构树，此时，如果 一个结点的权值符合要求，则其子树也符合要求。

如果不符合要求，这个点会被断开，即断开朋友关系。

可以通过一次 DFS 统计叶子节点数量来回答问题 2。

对于问题 3，除了修改本身，我还使用 vector 维护了所有的修改操作，在操作 1 时进行还原。

参考代码（重构树+倍增 LCA）。