Logo

菜单

prufer序列学习笔记

wjyppm
发布于 2025-08-23 / 8 阅读
0
0

0. 前言

邦邦卡邦！又学会了新的双射方式！这次是关于树的双射内容！

1. 定义与构建

1.1 定义

prufer 序列，又叫做 prüfer 序列，因为键盘平时不太好打出来 ü 所以一般叫做 prufer 序列。他的作用就是可以将一个有标号的 n 个点的树映射成一个由 n-2 个在 [1,n] 范围内的数所组成的序列，同时这个序列也会唯一对应一个树。也就是说，prufer 序列和树结构构成双射。

1.2 构建

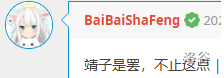
钦定 n 为树的根节点，因为这个树我没有说这是有根树，所以不会影响。

每次选择编号最小的叶子结点并删掉它，再把它的父亲的编号加入序列中。重复此操作，直到树上只有两个点为止。显然，这两个点中必有一个是编号最大的点 n。为什么是两个点呢？假设我们再进行一次操作，那么进入序列的必然是 n。这是没有意义的操作。而如果我们进行了这次操作，末尾不为 n 的 prufer 序列将失去对应一个树的优秀性质。

以下是一个 n=7 的例子：

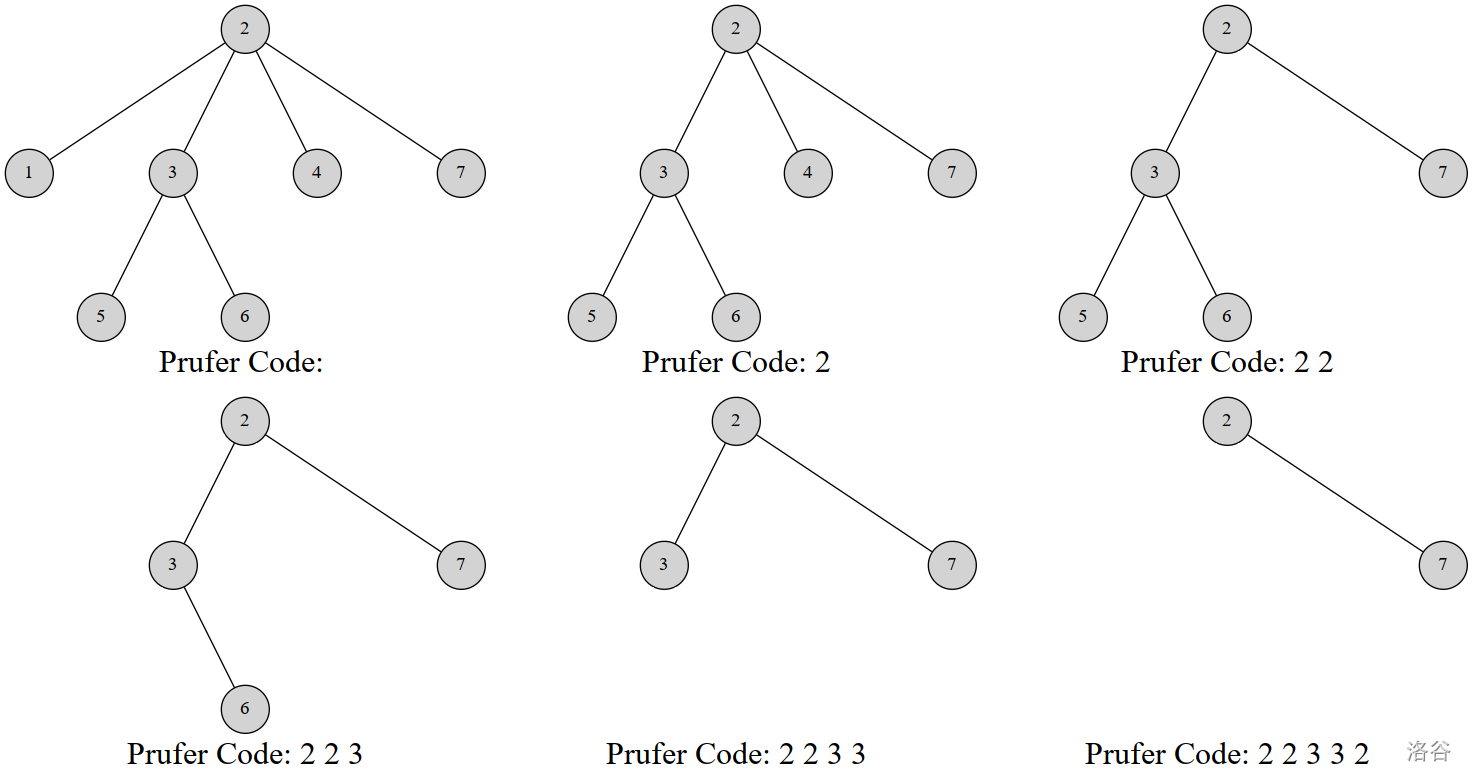
最终的序列就是 \{2,2,3,3,2\}。

1.3 还原

那么可以看得出来，经过此操作，每个树都对应了一个 prufer 序列。如果我么能从 prufer 序列还原出树，那么就证明了树和 prufer 序列是一一对应的。

prufer 序列有一个性质如下：

  • 树上每个点的度数等于在 prufer 序列上出现的次数加 1。

这个性质很好想，因为度数要么来自儿子要么来自父亲贡献，没删掉一个儿子，这个点就会在 prufer 序列上出现一次。而众所周知的是树上一个节点有且仅有一个父亲，所以出现次数加 1 就是度数。而对于根节点为 n 则不一样，它在 prufer 序列中出现的次数为它的儿子数减 1，即它的度数减 1。

有了这个性质，我们就可以得知没有出现在 prüfer 序列上的点，一定是叶子结点。

这样我们轻易就能得到树上最小的叶子结点的编号，就是没有在 prüfer 序列上出现的点。我们将这个叶子结点与 prüfer 序列上的第一个数连边，然后删除这个点和 prüfer 序列上的第一个数。如果将编号大于该叶子结点的编号减一，我们就得到了一个长度为 n-3 的 prüfer 序列，对应一个大小为 n-1 的树。因此可以使用同样的方法重复操作，再把最后剩下的点连向 n，就可以得到原树。

以下为 \{2,2,3,3,2\} 的构造：

  • 度数：dg[1,7]=\{1,4,3,1,1,1,1\}。
  • 取出 1，令 1\to 2，dg[1,7]=\{0,3,3,1,1,1,1\}。
  • 取出 4，令 4\to 2，dg[1,7]=\{0,2,3,0,1,1,1\}。
  • 取出 5，令 5\to 3，dg[1,7]=\{0,2,2,0,0,1,1\}。
  • 取出 6，令 6\to 3，dg[1,7]=\{0,2,1,0,0,0,1\}。
  • 取出 3，令 3\to 2，dg[1,7]=\{0,1,0,0,0,0,1\}。
  • prufer 序列遍历完，还剩下 n=7 和 2 号点，连接即可。

总连边：

1 2
4 2
5 3
6 3
3 2
7 2

可以自行验证，有结果：

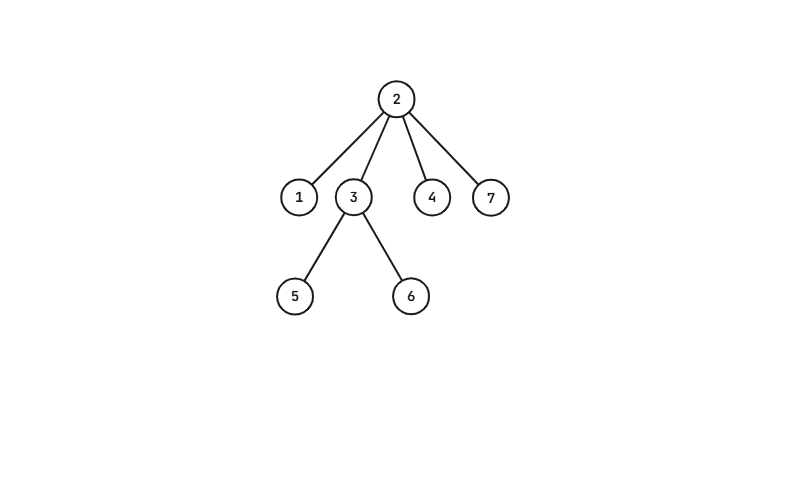
故证明成立。

1.4 线性时间做到构造与还原

显然可以使用堆做到 O(n\log n) 的复杂度，但其实有更优的做法。

维护一个下标 p，初始值为最小的叶结点编号。重复以下操作：

  1. 删除编号为 p 的结点，并检查是否使其父亲成为叶结点。
  2. 设其父亲的编号为 x。先将 x 加入序列。若 x 成为了新的叶子结点，判断其与 p 的大小关系。若 x<p，则立即删除 x，然后重复判断 x 的父亲；否则不管。
  3. 使 p 自增，直到 p 指向一个叶子结点为止。

因为每条边最多被访问一次（在删点的时候访问父亲），指针最多遍历每个点一次，所以复杂度是 O(n) 的。

这有点像可删堆的操作，可以结合理解。

对于还原类似，用同样的方法寻找编号最小的叶结点删除即可。

以下为 P6086 【模板】Prüfer 序列 的代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=5e6+15;
int fa[MN],dg[MN],p[MN],n,m,ans;

void TtoP(){
    for(int i=1;i<n;i++){
        cin>>fa[i];
        dg[fa[i]]++;
    }
    for(int i=1,x,j=1;i<=n-2;i++,j++){
        while(dg[j]) j++;
        p[i]=fa[x=j];
        while(i<=n-2&&!--dg[p[i]]&&p[i]<j){
            p[++i]=fa[x=fa[x]];
        }
    }
    for(int i=1;i<=n-2;i++){
        ans^=1ll*i*p[i];
    }
}

void PtoT(){
    for(int i=1;i<=n-2;i++){
        cin>>p[i];
        dg[p[i]]++;
        p[n-1]=n;
    }
    for(int i=1,x,j=1;i<=n-1;i++,j++){
        while(dg[j]) j++;
        fa[x=j]=p[i];
        while(i<=n-1&&!--dg[p[i]]&&p[i]<j) fa[x=fa[x]]=p[++i];
    }
    for(int i=1;i<=n-1;i++){
        ans^=1ll*i*fa[i];
    }
}

signed main(){
    cin>>n>>m;
    if(m==1){
        TtoP();
    }else PtoT();
    cout<<ans;
    return 0;
}

1.5 性质总结

说了这么多，我们来总结几个关键的性质来辅助做题。

  • Prufer 序列与树构成唯一双射，在计数问题中对一般树计数可以考虑直接对 prufer 序列计数。
  • 树上每个点的度数等于在 prufer 序列上出现的次数加 1。
  • 所有没在序列里出现过的点，一定是树中的叶子。
  • 对于完全图 K_{n} 有 n^{n-2} 颗生成树。（任意一个长度为 n-2 的值域 [1,n] 的序列计数）

我们对第四个结论进行推广：

  • n 个点形成有 k 颗树的有标号无根树森林，使得给定的 k 个点两两不属于同一棵树，此时的方案总数为 k\cdot n^{n-k-1}。
  • 指定点度数的生成树方案为 \dfrac{(n-2)!}{\prod_{i=1}^n (d_{i}-1)}。
  • 若 n 个点已经被连成大小为 \{s_{i}\}_{i=1}^k 的 k 个连通块，则在这些连通块之间加边构成生成树的方案数为 n^{k-2}\prod_{i=1}^k s_{i}。

推广 1 的证明：给定 n 个点和 k 个指定点，两两不在同一棵树的无根森林数：

  • 每个指定点作为不同树的根，有根森林数 n^{\,n-k}。
  • 无根森林对应有根森林，每棵树根可选择 k 种，调整得到：
k \cdot n^{\,n-k-1}.

推广 2 的证明：指定 n 点度数 \{d_i\} 的生成树数：

  • Prüfer 序列长度 n-2。
  • 每点 v_i 出现 d_i-1 次。
  • 多重排列计数：
\frac{(n-2)!}{\prod_{i=1}^n (d_i-1)!}.

推广 3 在后面例题会证明。

2. 例题

推广 2 P2290

显然。

推广 3 CF156D Clues

设 s_{i} 为第 i 个连通块的点数，d_{i} 表示连通块在树上的度数。

那么有 Prufer 序列方案数：

\dfrac{(k-2)!}{(d_{1}-1)!(d_{2}-1)!\dots (d_{n}-1)!}

而一个连通块连接边的方案为 \prod_{i=1}^k s_{i}^{d_{i}}。那么总方案数枚举 d_{i}乘起来即为：

\sum\limits_{d_{i}>1,\sum\limits_{i=1}^k d_{i}=2k-2}\dfrac{(k-2)!}{(d_{1}-1)!(d_{2}-1)!\dots (d_{n}-1)!} \prod_{i=1}^k s_{i}^{d_{i}}

设 e_{i}=d_{i}-1，有

\sum\limits_{e_{i}>0,\sum\limits_{i=1}^k e_{i}=k-2}\dfrac{(k-2)!}{e_{1}!e_{2}!\dots e_{k}!} \prod_{i=1}^k s_{i}^{e_{i}+1}

考虑多元二项式定理：

(x_1 + \dots + x_m)^p = \sum_{c_i \ge 0,\sum_{i=1}^m c_i = p}\binom{p}{c_1, c_2, \cdots ,c_m}\cdot \prod_{i=1}^m{x_i}^{c_i}

原式变为：

(s_1+s_2+\cdots+s_k)^{k-2}\cdot\prod_{i=1}^ks_i

即：

n^{k-2}\cdot\prod_{i=1}^ks_i

P2624 [HNOI2008] 明明的烦恼

只给了一些点的度数，对于给定度数点的排列方案数也是可以算出来的，记 sum=\sum\limits_{i=1}^n (d_{i}-1)，令 cnt 表示已知度数的点的个数。那么由上述推论 2 有：

\binom{n-2}{sum}\times \frac{sum!}{\prod_{i=1}^{cnt} (d_{i}-1)}

然后剩下的 n-cnt 个数任意插在 (n-sum-2) 的位置上即可，即 (n-cnt)^{n-sum-2}。答案就是乘起来即可，但是不给模数是有什么心事吗？我直接 python 喵了。

CF917D Stranger Trees

等会，题面这个图还有题目背景，莫非是？

咳咳，回到正题，首先看到 “恰好” 直接哈气。用二项式反演反演成至少，有：g_{k}=\sum\limits_{i=k} ^n \binom{i}{k} f_{i} \Leftrightarrow f_{k}=\sum\limits_{i=k}^n (-1)^{i-k} \binom{i}{k} g_{i}。其中 f 为答案，g 为至少 k 条边相同的方案数。

然后考虑 g 怎么算，发现这玩意我们把钦定的 i 条边断开，会形成 n-i 个连通块，而这些连通块都是独立树计数的。根据 Prufer 定理有任意连边方案数：

n^{m-2}\prod_{i=1}^m s_{i}

m 为连通块个数，其中 s_{i} 还是连通块大小。

然后考虑如何快速计算，发现如果直接做因为边不确定状压直接爆炸。数据范围 O(n^3)，考虑发掘性质。

我们考虑把 g_{k} 的组合意义拆分，前式子可以随便计算，而后面却要求我们快速不用状压计算。考虑 DP，设 f(i,j,k) 表示 i 子树内，分成了 j 个连通块，当前 i 所在连通块大小为 k 的方案数。时间复杂度 O(n^3) 可以 O(1) 转移但是我认为是 O(n^4)\to O(n^5) 就很难泵。

但是我们显然有更好的做法，考虑我们只是在计算 \prod_{i=1}^m s_{i}，考虑复杂度瓶颈就是在于这个 k 这一维度让我们的优化没有前途。考虑切换组合意义，发现 \prod_{i=1}^m s_{i} 的本质就是给每个连通块内部任意定根的方案数，把根是否确定放进状态中即可。

那么这很好考虑设 f(i,j,0/1) 表示 i 子树内，分成了 j 个连通块，i 所在连通块是否定根的方案数，转移用背包对子树合并即可，时间复杂度 O(n^2)。

Kruskal 重构树
Z 函数

评论